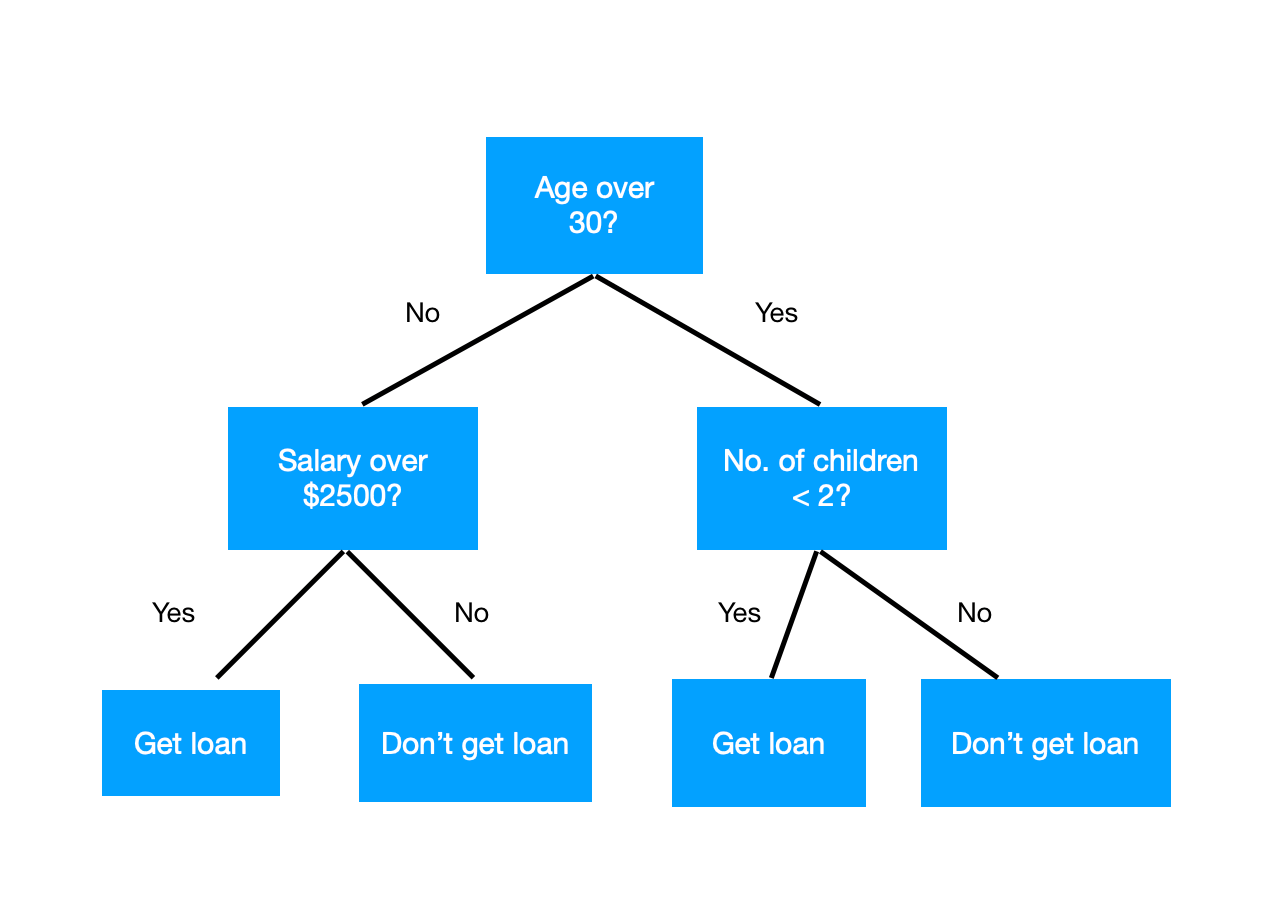
Idée
- Diviser récursivement l'espace
selon les valeurs des variables. - Prédire une nouvelle entrée en regardant
dans quelle cellule elle arrive.
Exemple : extrait iris
| Petal.Length | Species |
|---|---|
| 1.4 | setosa |
| 1.4 | setosa |
| 4.7 | versicolor |
| 4.5 | versicolor |
| 6.0 | virginica |
| 5.1 | virginica |
- Si Petal.Length <= 2, alors setosa
- Si 2 < Petal.Length < 5, alors versicolor
- Si Petal.Length >= 5, alors virginica.
Données + cibles + règles = arbre (...hmm)
clf = sklearn.tree.DecisionTreeClassifier()
# Note : numpy.reshape nécessaire ici...
res = clf.fit(iris.data[[0,1,50,51,100,101],2],
iris.target[[0,1,50,51,100,101]])
graphviz.Source(tree.export_graphviz(clf))Arbres...


...Avec un peu d'imagination !
Exemple complet(en R !)
library(titanic) ; library(rpart)
# Sélection des variables a priori pertinentes :
# type et prix du billet, âge, sexe. Cible = survie
fit = rpart(Survived ~ Pclass+Fare+Sex+Age,
titanic_train, method="class")
library(rpart.plot) ; rpart.plot(fit)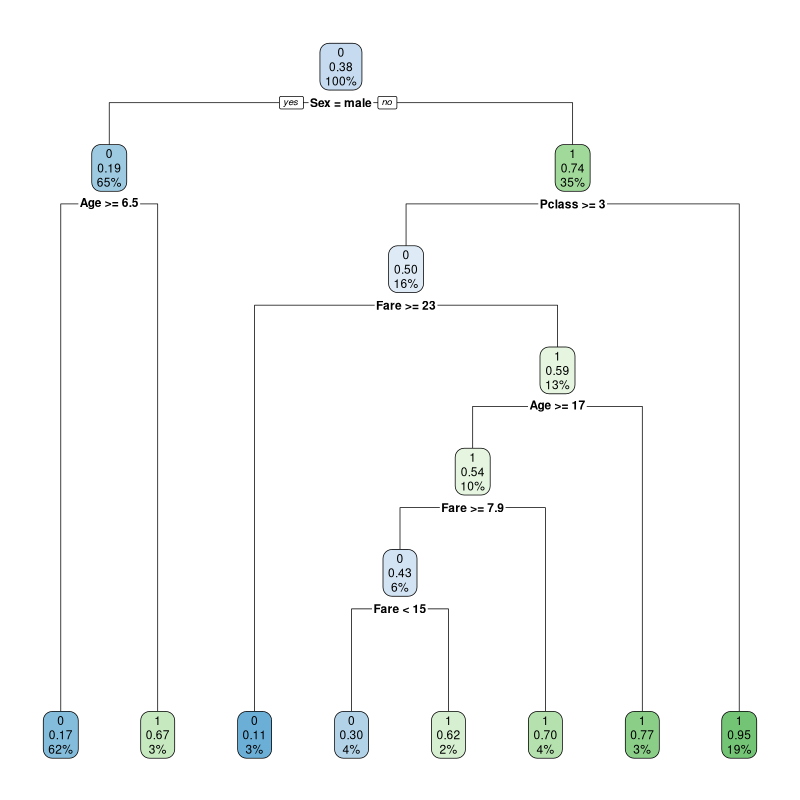
Algorithme
À partir des données complètes...
- Chercher la "meilleure" division (selon un attribut)
- Découper les données selon cette division
- Recommencer dans chaque subdivision
...Jusqu'à ce qu'aucune division ne soit possible.
Difficulté = point 1.
Cas d'un attribut numérique : 2 classes
| Température | Courir ? |
|---|---|
| 12 | oui |
| 18 | oui |
| 25 | oui |
| 27 | oui |
| 20 | non |
| 22 | non |
| 3 | non |
| -1 | non |
| Température | Courir ? |
|---|---|
| -1 | non |
| 3 | non |
| 12 | oui |
| 18 | oui |
| 20 | non |
| 22 | non |
| 25 | oui |
| 27 | oui |
Qualité d'une division
- Définition d'un indice $I$ évaluant l'hétérogénéité dans un ensemble.
- Qualité = $I - \alpha I_{gauche} - (1 - \alpha) I_{droite}$ ($\geq 0$).
(Le désordre ne peut que diminuer après division).
- Indice de Gini $I = 1 - \sum_{k=1}^{K} p_k^2$ avec
$p_k$ = proportion de la classe $k$. - Entropie (discrète) $I = - \sum_{k=1}^{K} p_k \log(p_k)$.
Découpage entre 18 et 20 : température <= 19 ou > 19.
4 lignes de chaque côté : proportions 4/8 et 4/8 (0.5).
2 "oui" et 2 "non" de chaque côté :
$G = 0.5 [ (2/4)^2 + (2/4)^2 ] + 0.5 [ (2/4)^2 + (2/4)^2 ]$
$\quad = 1/2$
Découpage entre 3 et 12 : température <= 7 ou > 7.
2 lignes à gauche, 6 à droite : proportions 2/8 et 6/8.
2 "non" à gauche, 2 "non" + 4 "oui" à droite :
$G = 2/8 [ (2/2)^2 + (0/2)^2 ] + 6/8 [ (2/6)^2 + (4/6)^2 ]$
$\quad = 2/3 > 1/2$
Cas d'un attribut numérique : 3 classes
| Température | Courir ? |
|---|---|
| 12 | oui |
| 18 | oui |
| 25 | oui |
| 27 | peut-être |
| 20 | non |
| 22 | non |
| 3 | peut-être |
| -1 | peut-être |
| Température | Courir ? |
|---|---|
| -1 | peut-être |
| 3 | peut-être |
| 12 | oui |
| 18 | oui |
| 20 | non |
| 22 | non |
| 25 | oui |
| 27 | peut-être |
Découpage entre 18 et 20 : température <= 19 ou > 19.
4 lignes de chaque côté : proportions 4/8 et 4/8 (0.5).
- À gauche : 2 "oui" + 2 "peut-être" + 0 "non"
- À droite : 1 "oui" + 1 "peut-être" + 2 "non"
$G = 0.5 [ (2/4)^2 + (2/4)^2 + (0/4)^2] +$
$\quad\quad 0.5 [ (1/4)^2 + (1/4)^2 + (2/4)^2 ]$
$\quad = 7/16$
Exercice : découpage entre 3 et 12 ?
Cas d'un attribut symbolique : 3 classes
| Météo | Courir ? |
|---|---|
| soleil | oui |
| soleil | oui |
| nuages | oui |
| nuages | peut-être |
| pluie | non |
| pluie | non |
| neige | peut-être |
| neige | peut-être |
Idée 1 : division "une valeur vs. les autres".
exemple : nuages vs. soleil/pluie/neige.
Idée 2 : tester toutes les combinaisons.
exemple : soleil/nuages vs. pluie/neige
Découpage soleil/nuages vs. pluie/neige.
4 lignes de chaque côté : proportions 4/8 et 4/8 (0.5).
- À gauche : 3 "oui" + 1 "peut-être" + 0 "non"
- À droite : 0 "oui" + 2 "peut-être" + 2 "non"
$G = 0.5 [ (3/4)^2 + (1/4)^2 + (0/4)^2] +$
$\quad\quad 0.5 [ (0/4)^2 + (2/4)^2 + (2/4)^2 ]$
$\quad = 9/16$
Exercice : découpage soleil/neige vs. nuages/pluie ?
Quelques détails
Potentiellement intéressant de découper en + d'un point, mais on se limite aux arbres binaires (plus simples, en général suffisants).
Si données manquantes :
- supprimer les lignes incomplètes ?
- estimer les valeurs manquantes ?
(moyenne, régression...) - propager la ligne d'un côté ou des deux ?
- préférer diviser sur un autre attribut ? (rpart)
Élagage
Diviser jusqu'à ne plus pouvoir = surapprentissage.
$\Rightarrow$ Paramètre de contrôle du nombre de divisions.
- Idée 1 : limiter a priori la profondeur
- Idée 2 : ne pas diviser si moins de $I$ individus
Mieux : fusionner les noeuds a posteriori
> fit = rpart(Species ~ ., iris, method="class",
control=list(minbucket=1,minsplit=2,cp=0))
> fit$cptable
CP nsplit rel_error xerror xstd
1 0.500 0 1.00 1.20 0.04898979
2 0.440 1 0.50 0.65 0.06069047
3 0.020 2 0.06 0.11 0.03192700
4 0.010 3 0.04 0.11 0.03192700
5 0.005 6 0.01 0.09 0.02908608
6 0.000 8 0.00 0.09 0.02908608Validation croisée
plotcp(fit)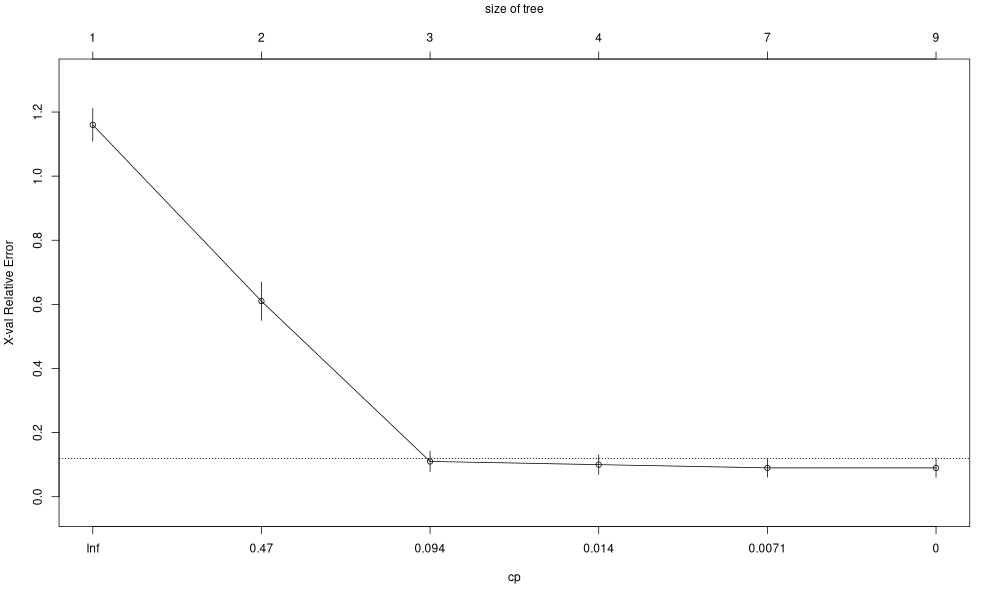
Régression
Au lieu de prédire une classe majoritaire, prédire la moyenne des valeurs présentes à cette feuille.
Changement dans l'algorithme : on cherche à minimiser la "variance" au lieu de maximiser $\sum p_k^2$.
Considérant une division comme précédemment,
$V = {\displaystyle \sum_{i \in G} (y_i - m_{G})^2 + \sum_{i \in D} (y_i - m_{D})^2}$
avec $m_G$ et $m_D$ moyennes à gauche et à droite.
Exemple : mensurations des poissons (extrait)
| Species | Length3 | Weight |
|---|---|---|
| Bream | 30.0 | 242 |
| Bream | 31.2 | 290 |
| Roach | 22.2 | 120 |
| Roach | 23.1 | 110 |
| Roach | 23.7 | 120 |
| Perch | 20.2 | 80 |
| Perch | 20.8 | 85 |
| Perch | 21.0 | 85 |
Poids en fonction de espèce et "longueur" ?
- Tri des lignes
- Évaluation en
chaque coupure - Division, retour en 1.
Attribut numérique
| Length3 | 20.2 | 20.8 | 21.0 | 22.2 | 23.1 | 23.7 | 30.0 | 31.2 |
|---|---|---|---|---|---|---|---|---|
| Weight | 80 | 85 | 85 | 120 | 110 | 120 | 242 | 290 |
Coupure entre 21 et 22.2 :
$V = (80 - m_G)^2 + 2 \times (85 - m_G)^2 +$
$V = $$(120 - m_D)^2 + \dots + (290 - m_D)^2$
Avec $m_G$ et $m_D$ moyennes à gauche / droite.
On trouve $V \simeq 28.10^3$
Attribut numérique - suite
Coupure entre 23.7 et 30 :
$V = (80 - m_G)^2 + \dots + (120 - m_G)^2 +$
$V = $$(242 - m_D)^2 + (290 - m_D)^2$
On trouve $V \simeq 2900 \ll 28000$
Conclusion: on coupe à $\frac{23.7 + 30}{2} = 26.85$
Attribut symbolique
| Species | Perch | Perch | Perch | Roach | Roach | Roach | Bream | Bream |
|---|---|---|---|---|---|---|---|---|
| Weight | 80 | 85 | 85 | 120 | 110 | 120 | 242 | 290 |
- Tri des groupes "Perch", "Roach", "Bream" par moyenne (Weight) $\nearrow$ : "Perch < Roach < Bream".
- Seulement deux divisions à considérer (pourquoi ?)
- Perch vs. Roach, Bream
- Perch, Roach vs. Bream
...Mène aux mêmes calculs.
En R
# En se limitant aux variables Species et Length3
fit = rpart(Weight ~ Species + Length3, Fish, method="anova")
# Avec toutes les variables
fit = rpart(Weight ~ ., Fish, method="anova")
rpart.plot(fit)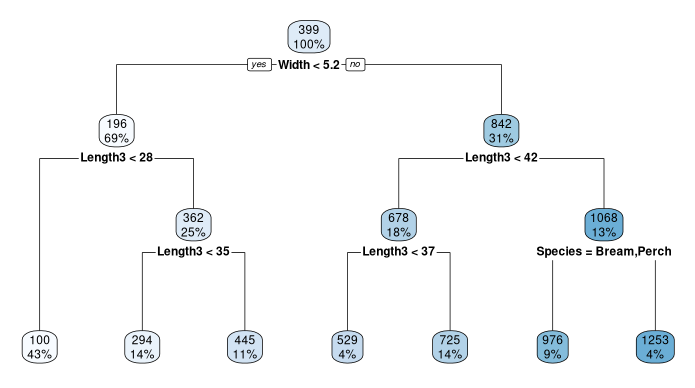
Élagage
plotcp(fit)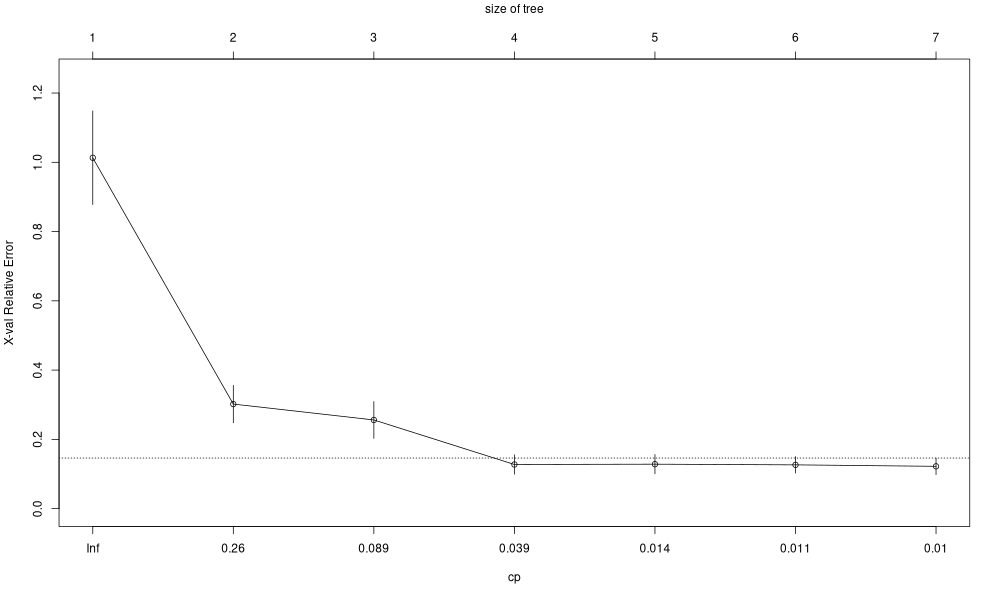
# En régression :
p <- predict(fit, newData, type="anova")
# En classification :
p <- predict(fit, newData, type="class")Exercice 1
Comparez les approches $k$ plus proches voisins et arbres de décision sur les jeux de données iris puis Fish (en classification).
Exercice 2
Dataset autos.
- Cherchez à prédire le prix d'une voiture
- Prenez le temps de comprendre les attributs, et prédisez par exemple "symboling".
Exercice 3
Récupérez le jeu de données adult (entraînement + test). L'ensemble d'entraînement comporte des données manquantes :
- Supprimez les lignes incomplètes, puis lancez rpart.
- Faites tourner rpart sur l'ensemble complet.
Dans les deux cas, il faut estimer l'erreur sur l'ensemble de test.
Conclusion ?