Bases des probabilités
Premier paragraphe du polycopié :
L'objet de la théorie des probabilités est de fournir un formalisme mathématique précis, propre à décrire des situations dans lesquelles intervient le "hasard", c'est-à-dire des situations dans lesquelles un certain nombre de conditions étant réunies (les causes), plusieurs conséquences sont possibles (les effets) sans que l'on puisse a priori savoir laquelle sera réalisée.
Probabilités = "mathématisation" du hasard
Intérêt des probabilités
Des applications nombreuses :
- Vie quotidienne
- Aux statistiques
- Théorie des jeux
- Économie, finance
- Physique (mécanique statistique...)
- Biologie
- Branche importante des mathématiques
- ...Etc
Introduction
- On lance 4 fois un dé à 6 faces, et gagne si au moins un six apparaît.
- On lance 24 fois deux dés à 6 faces, et gagne si un double six apparaît.

Quel jeu faut-il préférer ? Pourquoi ?
(Avant) Chevalier de Méré : "Les deux m'avantagent !"
(Après) Chevalier de Méré : "Heu, faut que je revoie mes calculs..."
Espace probabilisable
Espace fondamental (ou univers des possibles)
Ensemble de tous les résultats envisagés d'une expérience aléatoire, noté £\Omega£.
- trois lancers d'une même pièce de monnaie
- nombre d'essais pour atteindre le centre d'une cible
- durée de vie d'une ampoule
£\Rightarrow \Omega£ peut être fini, infini dénombrable ou non
Choix de £\Omega£
Il n'y a en général pas unicité du choix de £\Omega£
Difficulté : déterminer un univers £\Omega£ adapté au problème
Exemples pour le lancer de deux dés :- £\Omega = \{(1,1),(1,2),\dots,(6,5),(6,6)\}£, ensemble des couples formés par les deux chiffres (avec ordre)
- £\Omega = \{\{1,1\},\{1,2\},\dots,\{5,6\},\{6,6\}\}£, ensemble des ensembles formés par les deux chiffres (sans ordre)
- £\Omega = \{2,3,\dots,12\}£, ensemble des sommes possibles (si l'on ne s'intéresse qu'à la somme)
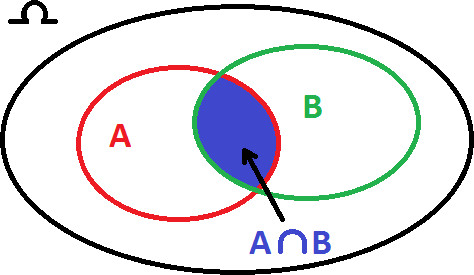
Évènements
Intuition : évènement = assertion relative au résultat d'une expérience. Cette assertion détermine une partie de £\Omega£.
Évènement
Un évènement A est une partie de £\Omega£ : £A \in \cP(\Omega)£.
Évènement élémentaire si £A£ réduit à un seul élément.
- £A = \{6\}£ (un six)
- £B = \{2,4,6\}£ (numéro pair)
- £C = \{4,5,6\}£ (numéro £\geq£ 4)
Terminologie des évènements aléatoires
Évènement = sous-ensemble de £\Omega£, élément de £\cP(\Omega)£.
| Langage probabiliste | Notation | Langage ensembliste |
|---|---|---|
| issue ou résultat | £\omega£ £(\in \Omega)£ | élément de £\Omega£ |
| évènement £A£ | £A \subseteq \Omega£ | partie de £\Omega£ |
| £A£ est réalisé | £\omega \in A£ | appartenance |
| évènement contraire (non £A£) | £\overline A = \Omega \backslash A£ | complémentaire |
| £A£ et £B£ | £A \cap B£ | intersection |
| £A£ ou £B£ | £A \cup B£ | union |
| évènements incompatibles | £A \cap B = \emptyset£ | disjoints |
| £A£ implique £B£ | £A \subseteq B£ | inclusion |
| évènement impossible | £\emptyset£ | ensemble vide |
| évènement certain | £\Omega£ | partie maximale |
| système complet £A_1,\dots,A_n£ | £\Omega = \sqcup A_i£ | partition |
Exemple
Deux serveurs informatiques £S_1£ et £S_2£
Évènements considérés :- £A_1£ (resp. £A_2£) : le premier (resp. second) serveur fonctionne
- £B_k£ : exactement £k£ serveurs sont opérationnels
- £C£ : au moins un serveur est en ligne
Réexpressions de £B_k£ et £C£
- £B_0 = \overline{A_1} \cap \overline{A_2}£
- £B_1 = (A_1 \cap \overline{A_2}) \cup (\overline{A_1} \cap A_2)£
- £B_2 = A_1 \cap A_2£
- £C = A_1 \cup A_2£
Propriétés
Associativité, commutativité de £\cup£ et £\cap£.
Distributivité : ££A_1 \cap (A_2 \cup A_3) = (A_1 \cap A_2) \cup (A_1 \cap A_3)££ ££A_1 \cup (A_2 \cap A_3) = (A_1 \cup A_2) \cap (A_1 \cup A_3)££
Lois de De Morgan : ££\overline {A_1 \cap A_2} = \overline {A_1} \cup \overline {A_2}££ ££\overline {A_1 \cup A_2} = \overline {A_1} \cap \overline {A_2}££
Espace probabilisable
Tribu
Une tribu ou £\sigma£-algèbre sur £\Omega£ est un ensemble £\cT£ vérifiant les propriétés suivantes
- £\Omega \in \cT£
- Stabilité par passage au complémentaire : £\forall A \in \cT£, £\Omega \backslash A \in \cT£
- Stabilité par union finie ou dénombrable : £\forall (A_n) \subseteq \cT£, £\cup_i A_i \in \cT£
On appelle espace probabilisable le couple £(\Omega, \cT)£ où £\cT£ constitue une tribu de parties de £\Omega£
Remarque : une tribu ne contient pas nécessairement les évènements élémentaires
Définition / Exemple
Tribu engendrée par ²S \subseteq E²
Plus petite ²\sigma²-algèbre sur ²E² contenant tous les éléments de ²S²
La tribu borélienne sur ²\R² est la ²\sigma²-algèbre engendrée par les intervalles
Elle contient en particulier tous les intervalles, leurs unions ...etc, mais aussi des ensembles plus exotiques : ²²\left\{\begin{align*} \cT([a,b]) &= \left[a, \frac{a+b}{3}\right] \cup \left[b - \frac{a+b}{3}, b\right]\\ \bigcap_{n \in \N} \cT^n([0,1]) &= \mbox{ ensemble de Cantor} \end{align*} \right.²²
Mesure de Lebesgue sur ²\R²
Algèbre (de parties) = ensemble de parties de ²\R² contenant ²\emptyset² et ²\R², stable par passage au complémentaire et par réunion finie.
Mesure positive ²\nu² sur une algèbre ²\cA² :- ²\nu(\emptyset) = 0²
- Pour toute suite ²(A_n)² de parties de ²\cA² 2 à 2 disjointes : ²\nu \left( \sqcup A_k \right) = \sum \nu(A_k)²
On considère l'algèbre ²\cA² des réunions finies d'intervalles de ²\R². Pour ²A \in \cA² on pose ²\nu_0(A) = \sum_{]\negthinspace[ a_k, b_k ]\negthinspace[ \in A} (b_k-a_k)². Alors il existe une unique mesure positive sur ²(\R, \cB(\R))² coïncidant avec ²\nu_0² : c'est la mesure de Lebesgue.
Pour les détails, voir par exemple ce document
Boréliens ²\subsetneq² ensemble mesurables ²\subsetneq \cP(R)²
Ensemble mesurable non borélien
L'ensemble des nombres s'écrivant ²²x = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{\ddots\,}}}²² avec ²a_{i_0}² divise ²a_{i_1} \dots² divise ²a_{i_k} \dots² pour une suite extraite ²(a_{i_k})²
Ensemble de Vitali : non mesurable
Classes d'équivalence sur ²[0,1]² pour la relation ²x \sim y \Leftrightarrow x - y \in \Q². ²²cl(0) = [0,1] \cap \Q \, , \quad cl\left(\frac{\pi}{4}\right) = [0,1] \cap \left\{ \frac{\pi r}{4 s} \, / \, r,s \in \N^* \right\} \, \dots²²
Autres exemples dans ce chapitre.
Remarque / Exercice
Soit ²C = \{ \{\omega\}, \omega \in \Omega \}². Montrer que
²\sigma(C) = \cP(\Omega) \Leftrightarrow \Omega² au plus dénombrable.
(Référence : Ex.7 ch.2 dans Calcul des probabilités de D. Foata et A. Fuchs)
²\Leftarrow² : toute partie de ²\Omega² est réunion au plus dénombrable de singletons
²\Rightarrow² : soit ²\cT² l'ensemble de toutes les parties au plus dénombrables ou de complémentaire au plus dénombrable. C'est une tribu, qui contient tous les singletons. Donc ²C \subseteq \cT², puis ²\sigma(C) \subseteq \cT². Si ²\Omega² était indénombrable on trouverait ²\Omega_1² et ²\Omega_2² indénombrables vérifiants ²\Omega = \Omega_1 \sqcup \Omega_2².
Remarque
L'intersection de deux tribus est une tribu, mais
La réunion de deux tribus n'est pas nécessairement une tribu
Contre-exemple
²\Omega = \{1,2,3,4,5,6\}²
²\cT_1 = \{\emptyset, \Omega, \{1,2\}, \{3,4\}, \{5,6\},²
²\cT_1² = ²\{1,2,3,4\}, \{1,2,5,6\}, \{3,4,5,6\}\}²
²\cT_2 = \{\emptyset, \Omega, \{1,2,3\}, \{4,5,6\} \}²
²\cT_1 \cup \cT_2² contient ²\{1,2\}² et ²\{4,5,6\}² mais pas ²\{1,2,4,5,6\} = \overline{\{3\}}²
Espace probabilisé
Probabilité
Soit £(\Omega, \cT)£ un espace probabilisable. Une probabilité est une application £\P£ réelle définie sur £\cT£ vérifiant les trois axiomes suivants appelés axiomes de Kolmogorov
- £\P : \cT \rightarrow \R^+£
- £\P(\Omega) = 1£
- Pour des évènements £A_i£ deux à deux incompatibles avec £i \in I \subseteq \N£ ££\P\left(\bigsqcup A_i\right) = \sum \P(A_i)££
- £(\Omega, \cT)£ un espace probabilisable,
- £\P£ une probabilité sur £\cT£.
Propriétés
Pour tout £(A,B) \in \cT^2£
- £\P(\Omega) = 1, \P(\emptyset) = 0£
- £\P(\overline A) = 1 - \P(A)£
- £\P(A) \in [0,1]£
- £\P(A \cup B) = \P(A) + \P(B) - \P(A \cap B)£
- £A \subseteq B \Rightarrow \P(A) \leq\P(B)£
Théorème des probabilités totales
Soit £\{B_i, i \in I \subseteq \N\}£ un système complet d'évènements.
££\P(A) = \sum \P(A \cap B_i)££
Remarque / Exercice
Soit ²(\Omega, \cT, \P)² un espace probabilisé. On note ²A \Delta B = (A \cap \overline{B}) \cup (\overline{A} \cap B)² la différence symétrique d'ensembles. Montrer que ²\P(A \Delta B)² définit une distance "probabiliste" sur ²\cT².
(Source : Ex.5 ch.3 dans Calcul des probabilités de D. Foata et A. Fuchs)
Symétrie, positivité : clair.
Séparation : ²\P(A \Delta B) = 0²
Séparation : ²\quad \Leftrightarrow \P(A \cap \overline{B}) = 0 \mbox{ et } \P(\overline{A} \cap B) = 0²
Séparation : ²\quad \Leftrightarrow A \subseteq B \mbox{ et } B \subseteq A \Leftrightarrow A = B \quad \boxed{p.s.}²
Inégalité triangulaire : ²A \Delta C \subseteq A \Delta B \cup B \Delta C \, , \dots²
Note : on a aussi ²|\P(A) - \P(B)| \leq \P(A \Delta B)² :
²\P(A \Delta B) = \P(A) + \P(B) - 2 \P(A \cap B) \, , \dots²
Remarques
Une union au plus dénombrable d'évènements impossibles est impossible. ££\P(A_n) = 0 \Rightarrow \P\left(\bigcup A_n\right) = 0££
Une intersection au plus dénombrable d'évènements certains est certaine. ££\P(A_n) = 1 \Rightarrow \P\left(\bigcap A_n\right) = 1££
Inégalité de Boole
Pour toute famille d'évènements £(A_n)_{n \in I \subseteq \N}£, ££\P\left(\bigcup A_n \right) \leq \sum_I \P(A_n)££
Formule du crible
Soient ²A_1, \dots, A_n² des évènements ²²\P(A_1 \cup \dots \cup A_n) = \sum_{k=1}^{n} (-1)^{k-1} \sum_{1 \leq i_1 < \dots < i_k \leq n} \P(A_{i_1} \cap \dots \cap A_{i_k})²²
Application
Un facteur pressé dépose ²n² enveloppes (de destinataires distincts) dans ²n² boîtes aux lettres différentes au hasard. Quelle est la probabilité que personne n'ait son courrier ?
²A_k² = la ²k^{\mbox{eme}}² personne a son courrier.
²²\begin{align*}
\P(\cap \overline{A_k}) &= 1 - \sum_{k=1}^{n} (-1)^{k-1} \sum_{1 \leq i_1 < \dots < i_k \leq n} \frac{(n-k)!}{n!}\\
&= \sum_{k=0}^{n} \frac{(-1)^k}{k!}
\end{align*}²²
Limites monotones
Pour toute suite croissante d'évènements £C_n£ (i.e. £\forall n \in \N£, £C_n \subseteq C_{n+1}£) : ££\P\left(\bigcup_{n=0}^{+\infty} C_n\right) = \lim_{n \to +\infty} \P(C_n)££
Et, pour toute suite décroissante d'évènements £D_n£ : ££\P\left(\bigcap_{n=0}^{+\infty} D_n\right) = \lim_{n \to +\infty} \P(D_n)££
Application
Soit £\Omega = [0,1]£, £\cT£ la tribu engendrée par les intervalles fermés, et £\P([a,b]) = b-a£ (tirage uniforme). Alors les intervalles £]a,b[£ sont aussi dans £\cT£, et ££ \begin{align*} \P(]a,b[) & = \P\left( \bigcup_{n > 2/(b-a)} \left[a+\frac{1}{n}, b-\frac{1}{n}\right] \right)\\ & = \lim_{n \to +\infty} \P([a+n^{-1}, b-n^{-1}])\\ & = \lim_{n \to +\infty} b - a - \frac{2}{n}\\ & = b - a \end{align*} ££
Équiprobabilité
Quand £\Omega£ est de cardinal fini on dit qu'il y a équiprobabilité quand les évènements élémentaires ont tous la même probabilité : £\P(\omega_i) = \frac{1}{n}£ avec £n = \# \Omega£.
En choisissant £B_i = \omega_i£ dans le théorème des probabilités totales, ££\forall A \in \cT, \, \P(A) = \frac{\# A}{\# \Omega} = \frac{\# \mbox{cas possibles}}{\# \mbox{cas favorables}}££
Le calcul des probabilités dans ce cas se ramène à des calculs de dénombrement
Rappels en combinatoire
- Nombre de permutations d'un ensemble à n éléments : £n!£
- Nombre de p-uplets d'un ensemble à n éléments : £n^p£
- Nombre de p-arrangements d'un ensemble à n éléments : £A_n^p = \frac{n!}{(n-p)!}£
- Nombre de parties d'un ensemble à n éléments : £2^n£
- Nombre de parties à p éléments d'un ensemble à n éléments : £C_n^p = \frac{n!}{p!(n-p)!} = \binom{n}{p}£
Formule du binôme de Newton : £(a+b)^n = \sum_{k=0}^n \binom{n}{k} a^k b^{n-k}£
Les paris du chevalier de Méré
Son raisonnement
Le jeu m'avantage si j'ai 4 fois 1 chance sur 6 de gagner. Il m'avantage donc de la même façon si j'ai ²6 \times 4=24² fois 1 chance sur ²6 \times 6=36² de gagner.
Analyse
Choix de £\Omega = \{ (a,b,c,d), 0 \leq a,b,c,d \leq 6 \}£, ensemble des combinaisons à quatre éléments entre 1 et 6 (avec ordre)
Lancers indépendants + dé non pipé £\Rightarrow£ équiprobabilité
Cas défavorables : 5^4. Cas possibles : 6^4
Probabilité recherchée = £1 - \frac{5^4}{6^4} > \frac{1}{2}£
...Même raisonnement pour deux dés et 24 lancers :
Probabilité recherchée = £1 - \frac{35^{24}}{36^{24}} < \frac{1}{2}£ (!)
Probabilités conditionnelles, indépendance
Contexte : information partielle, "£A£ est réalisé"
Probabilité conditionnelle
Soit £(\Omega,\cT,\P)£ un espace probabilisé et £A£ un évènement possible (£\P(A) > 0£). L'application ££ \P_A = \left\{ \begin{array}{ccccc} \cT&\rightarrow&[0,1]\\ B&\mapsto&\P_A(B) = \frac{\P(A \cap B)}{\P(A)} \end{array} \right. ££ est une probabilité sur £(\Omega,\cT)£ appelée probabilité conditionnelle sachant A
Notation courante : £\P_A(B) = \P(B|A)£
Remarque : £\P(A \cap B) = \P(A) \P(B|A)£
Formule des probabilités composées
Soient £A_1,\dots,A_n£ des évènements vérifiant £\P(A_1 \cap A_2 \cap \dots \cap A_n) > 0£. Alors ££ \begin{align*} \P(A_1\cap A_2\cap\dots \cap A_n) = \P(&A_1) \P(A_2|A_1) \P(A_3|A_1\cap A_2)\\ & \dots \P(A_n|A_1\cap A_2\cap \dots \cap A_{n-1}) \end{align*} ££
Formule des probabilités totales
Soient £(\Omega,\cT,\P)£ un espace probabilisé et £\{A_i, i \in I \subseteq \N\}£ un système complet d'évènements possibles. Alors, pour tout évènement B : ££ \begin{align*} \P(B) &= \sum_{i \in I} \P(A_i)\P(B|A_i)\\ &= \P(A_1)\P(B|A_1)+\dots+\P(A_n)\P(B|A_n) \end{align*} ££
Application
On recherche la probabilité d'attendre le RER moins de 5 minutes, notée £A£.
On dispose de :- £\P(A|P) = 0.8£ avec £P£ = "heure de pointe",
- £\P(A|J) = 0.5£ avec £J£ = "journée" (hors période de pointe),
- £\P(A|N) = 0.3£ avec £N£ = "nuit" (> 21h, < 6h).
On estime £\P(P) = 4/20£ (4h par jour), £\P(J) = 11/20£ et £\P(N) = 5/20£.
Alors si on prend le train à un instant aléatoire entre 5h et 1h : ££ \begin{align*} \P(A) & = \P(A|P)\P(P) + \P(A|J)\P(J) + \P(A|N)\P(N)\\ & = 0.8 \times 0.2 + 0.5 \times 0.55 + 0.3 \times 0.25\\ & = 0.51 \end{align*} ££
Indépendance
Deux évènements £A£ et £B£ sont (stochastiquement) indépendants si ££\P(A \cap B) = \P(A) \times \P(B)££
Des évènements £A_i£, £i \in I£ sont (mutuellements) indépendants si pour tout ensemble fini £J \subseteq I£, ££\P\left(\bigcap_J A_j \right) = \prod_J \P(A_j)££ (Notion plus forte que l'indépendance 2 à 2)
Indépendance de tribus
Des tribus ²(\cT_i)_{i \in I}² sont indépendantes si pour tout ensemble fini ²J \subseteq I² ²²\forall (A_j)_{j \in J} \in \prod_{j \in J} \cT_j \, , \quad \P\left(\bigcap_J A_j \right) = \prod_J \P(A_j) ²²
Remarque
L'indépendance d'une famille d'évènements ²(A_i)² équivaut à l'indépendance des tribus engendrées ²\sigma(A_i) = \{\emptyset, \Omega, A_i, \overline{A_i}\}²
Formules de Bayes
Première version
Soient deux évènements possibles £A£ et £B£. ££\P(A|B) = \frac{\P(B|A)\P(A)}{\P(B)}££
Seconde version
Soit £\{A_i, i\in I\subseteq \N\}£ un système complet d'évènements possibles, et £B£ vérifiant aussi £\P(B) > 0£. ££\P(A_k|B) = \frac{\P(B|A_k)\P(A_k)}{\P(B)} = \frac{\P(B|A_k)\P(A_k)}{\sum_I \P(B|A_i) \P(A_i)}££
Application
On reprend les données de l'exemple du RER, et suppose que quelqu'un a attendu plus de 5 minutes. Quelle information a-t-on sur l'horaire auquel il a pris le train ?
On cherche £\P(J|\overline{A})£ (par exemple). ££ \begin{align*} \P(J|\overline{A}) & = \frac{\P(\overline{A}|J) \P(J)}{\P(\overline{A})}\\ & = \frac{(1 - \P(A|J)) \P(J)}{1 - \P(A)}\\ & \simeq 0.56 \end{align*} ££
Compléments
Limites sup et inf
Soit £(A_n)_{n \in \N}£ une suite (quelconque) d'évènements. Alors les limites sup et inf sont respectivement égales à ££\overline{\lim}_{n \in \N} A_n = \bigcap_{n \in \N} \bigcup_{i \geq n} A_i££ ££\underline{\lim}_{n \in \N} A_n = \bigcup_{n \in \N} \bigcap_{i \geq n} A_i££
- £(\overline{\lim} A_n)^c = \underline{\lim} A_n^c£ , £(\underline{\lim} A_n)^c = \overline{\lim} A_n^c£
- ²\underline{\lim} A_n \subseteq \overline{\lim} A_n², avec égalité si £(A_n)£ est une suite monotone
Lemme de Borel-Cantelli
Soit £(A_n)_{n \in \N}£ une famille d'évènements.
- Si £\sum_{n \in \N} \P(A_n) < +\infty£, alors £\P(\overline{\lim} A_n) = 0£.
- Si les £A_n£ sont indépendants et £\sum_{n \in \N} \P(A_n) = +\infty£, alors £\P(\overline{\lim} A_n) = 1£.
Démonstration du 1. : £\overline{\lim} A_n \subseteq \cup A_n£, et £\P(\cup A_n) \leq \sum \P(A_n)£.
Inégalités utiles :- £\forall x > -1, \ln(1+x) \leq x£
- £\forall x \in \R, \exp(x) -1 \geq x£
Application 1
On effectue une série de lancers d'une pièce de monnaie équilibrée, et cherche £\P(A)£ avec A = "obtenir pile en temps fini".
££ \begin{align*} \P(A) & = \P(\exists n \in \N^* / ``\mbox{on obtient pile au n}{}^{eme}\mbox{ lancer}")\\ & = \P\left(\bigcup_{n \in \N^*} A_n \right) \mbox{ ,} \end{align*} ££ avec £A_n£ l'évènement "on obtient pile au £n^{eme}£ lancer".
- £\P(\overline{\lim}_{n \in \N^*} A_n) = 1£ (Borel-Cantelli)
- Donc £\P(A) = 1£ (et l'évènement se réalise une infinité de fois)
Application 2
Marche aléatoire sur Z
On part de 0, et effectue un pas à droite (+1) avec probabilité £p£, et un pas à gauche (-1) avec probabilité £q = 1-p£. Reviendra-t-on en zéro ?
£A_n£ = "revenir en 0 après £2n£ pas"
Cas favorables : £C_{2n}^n£, nombre de combinaisons de £n£ éléments parmi £2n£
£n£ pas à droite + £n£ pas à gauche £\Rightarrow \P(A_n) = C_{2n}^n p^n q^n£.
£\P(A_n) \simeq \frac{(4pq)^n}{\sqrt{\pi n}}£ via la formule de Stirling £m! \sim (\frac{m}{e})^m \sqrt{2\pi m}£
Deux cas
- £p \neq \frac{1}{2}£ : alors £\sum \P(A_n) < +\infty£, et £\P(\overline{\lim} A_n) = 0£
- £p = \frac{1}{2}£ : alors on repasse une infinité de fois en zéro, mais le lemme ne s'applique pas...
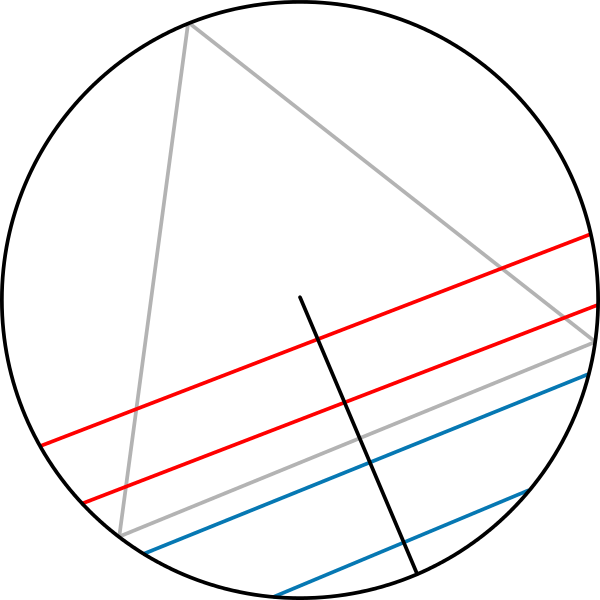
Paradoxe de Bertrand
Soit ²\cC² le cercle centré en 0 de rayon 1. On note ²\ell² la longueur du côté du triangle équilatéral inscrit dans ²\cC². On tire une corde du cercle "au hasard" et on souhaite calculer la probabilité que cette corde ²C² soit de longueur ²|C|² supérieure à ²\ell².
²\P(|C| \geq \ell) = ² ?
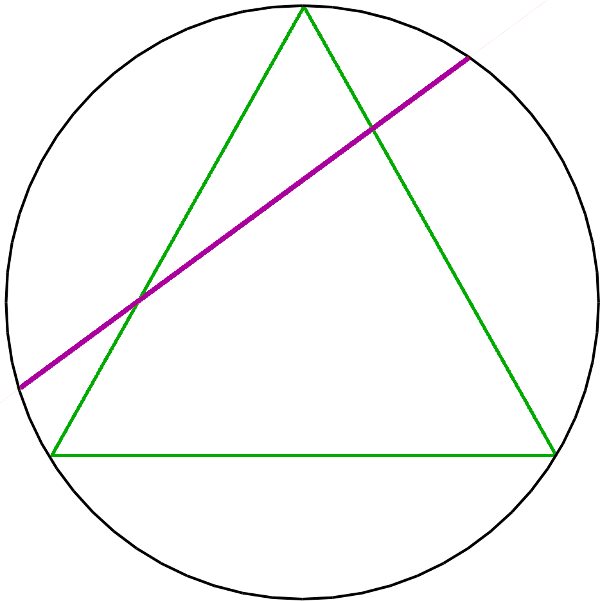
Premier calcul
On fixe un point sur le cercle, et tire au hasard un second. Par symétrie on obtient toutes les cordes ²C² possibles, et le secteur angulaire vérifiant la condition ²|C| \geq \ell² est d'amplitude ²\frac{\pi}{3}².
²\P(|C| \geq \ell) = \frac{1}{3}²
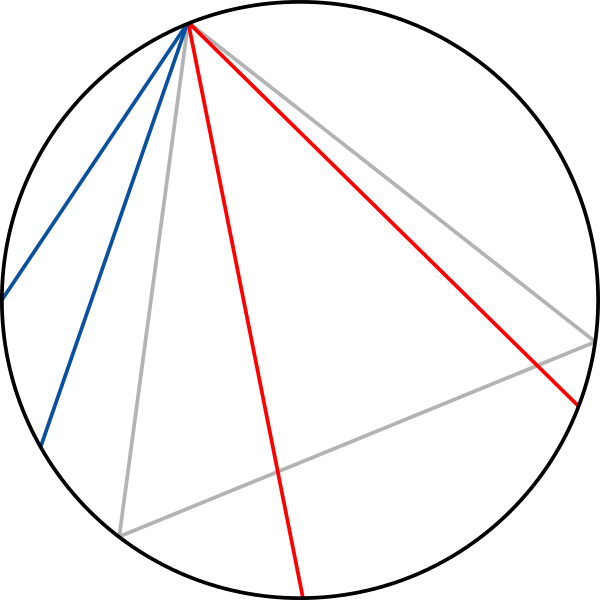
Second calcul
On choisit un point ²M² au hasard dans le disque, auquel on associe la corde passant par ²M² orthogonale à ²OM², ²O² étant le centre du cercle.
²|C| \geq \ell \Leftrightarrow M² est dans le cercle inscrit
Celui-ci est de rayon ²\frac{1}{2}², donc
²\P(|C| \geq \ell) = \frac{(1/2)^2}{1^2} = \frac{1}{4}²
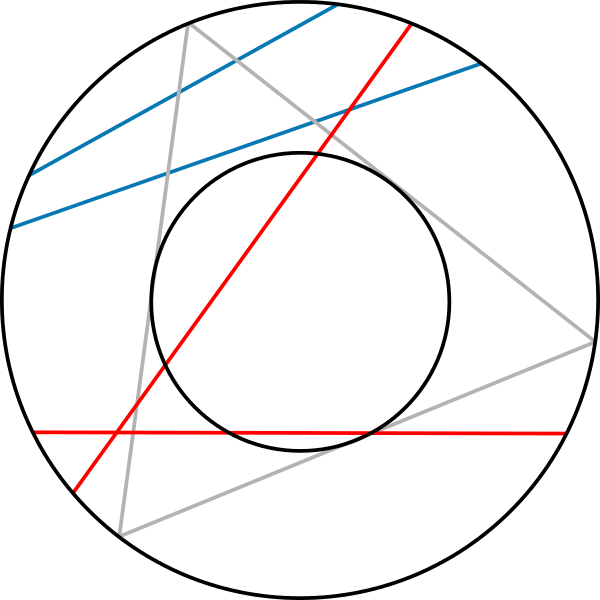
Troisième calcul
On fixe un rayon, puis on choisit un point au hasard sur celui-ci, qui sera le centre de la corde (rayon = médiatrice). Par symétrie on obtient toutes les cordes possibles, et seule la moitié "intérieure" du rayon vérifie la condition.
²\P(|C| \geq \ell) = \frac{1}{2}²
/