Variables aléatoires réelles
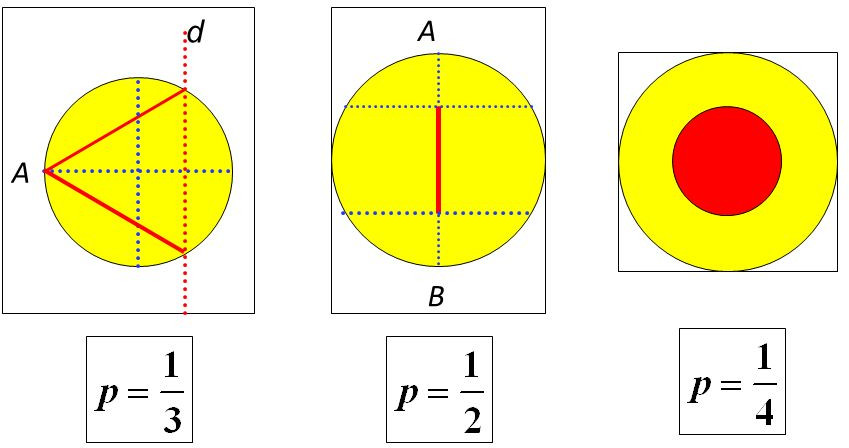
Introduction
Dans de nombreuses situations, on ne s’intéresse pas directement aux évènements aléatoires eux-mêmes, mais à des grandeurs numériques qui leur sont associées : nombre de particules émises par un élément radioactif, dans une direction et durant un intervalle de temps donné, puissance moyenne d’un "bruit" accompagnant la réception d'un signal radio, etc.
²\Rightarrow² On n'explicite pas les évènements ²A \in \cT² : ceux-ci sont quantifiés via leurs images par une certaine fonction ²X².
Exemple
- ²\Omega² = ensemble des conditions déterminant la taille d'un individu
- Observations = tailles des individus = ²X(\omega \in \Omega)²
On considère alors un univers des possibles réduit à ²X(\Omega)².
Définition
Étant donné un espace probabilisé £(\Omega, \cT, \P)£, on appelle variable aléatoire réelle une application £X£ définie sur £\Omega£ à valeurs dans £\R£, telle que l'image réciproque par £X£ de tout borélien de £\R£ soit un élément de la tribu £\cT£.
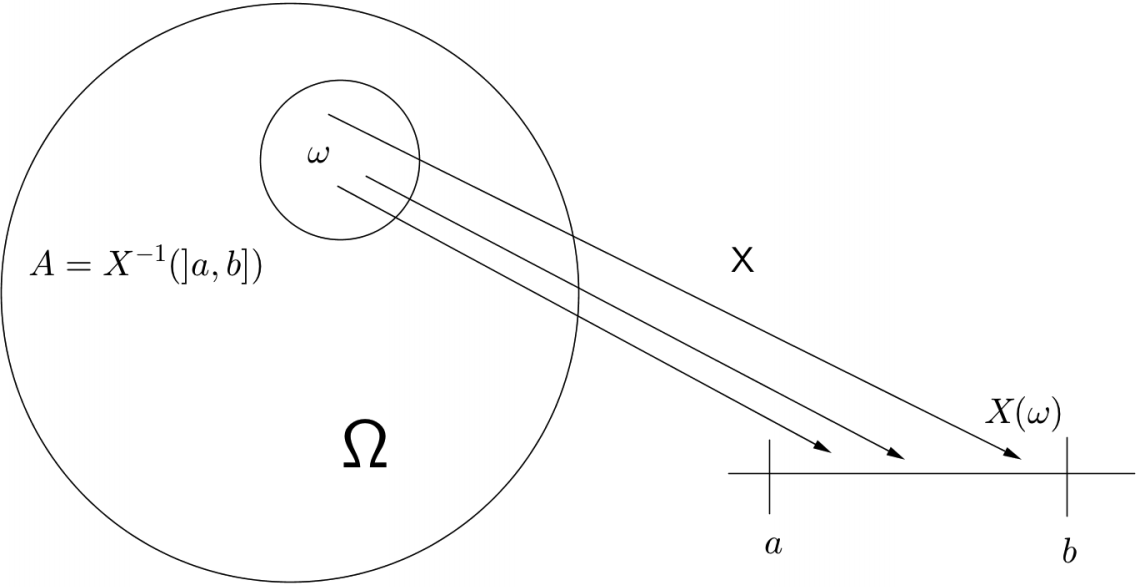
££X : \left\{ \begin{align*} \Omega & \rightarrow \R, \quad \quad \mbox{vérifiant } X^{-1}(]a,b]) \in \cT\\ \omega & \mapsto X(\omega) \end{align*} \right. ££
Exemples
Lancer de deux dés
£\Omega = \{1,\dots,6\}^2£, £\cT = \cP(\Omega)£, £\P(A \in \cT) = \frac{\#A}{36}£.
£X(\omega = (\omega_1,\omega_2)) = \omega_1 + \omega_2£
£X^{-1}(\{4\}) = \{\{1,3\},\{2,2\},\{3,1\}\}£
£\P(X^{-1}(\{7\}) = \P(X = 7) = \frac{6}{36} = \frac{1}{6}£
Indices de pollution
£\Omega = \{£ "Tous les paramètres aléatoires influents" £\}£ (température, vitesse du vent £\dots£)
£\cT = £ ? £\P(A \in \cT) = £ ? £X(\omega \in \Omega)£ = indice de pollution
£\P(X \in B)£ = ? (En pratique on cherche à modéliser £X£)
Exemple : 3 lancers d'une pièce
On cherche les probabilités d'obtenir £k£ fois face.
Modélisation via tribu triviale
£\Omega = \{F,P\}^3£
£\cT = \cP(\Omega) = \sigma(\{\omega \in \Omega\})£
£X : \omega \in \Omega \mapsto \sum_{i=1}^3 \1_{\omega_i = F}£
£\sigma(X^{-1}(B)) \subsetneq \cP(\Omega) \Rightarrow£ Tribu mieux adaptée
££\begin{align*} \cT = \sigma(&\{FFF\},\\ &\{FFP, FPF, PFF\},\\ &\{FPP, PFP, PPF\},\\ &\{PPP\}) \end{align*}££
Voir aussi le site mathsisfun.
Loi de probabilité et moments
Définitions, propriétés
Probabilité image
On appelle loi de probabilité de £X£ la probabilité £P_X£, image de £\P£ par £X£.
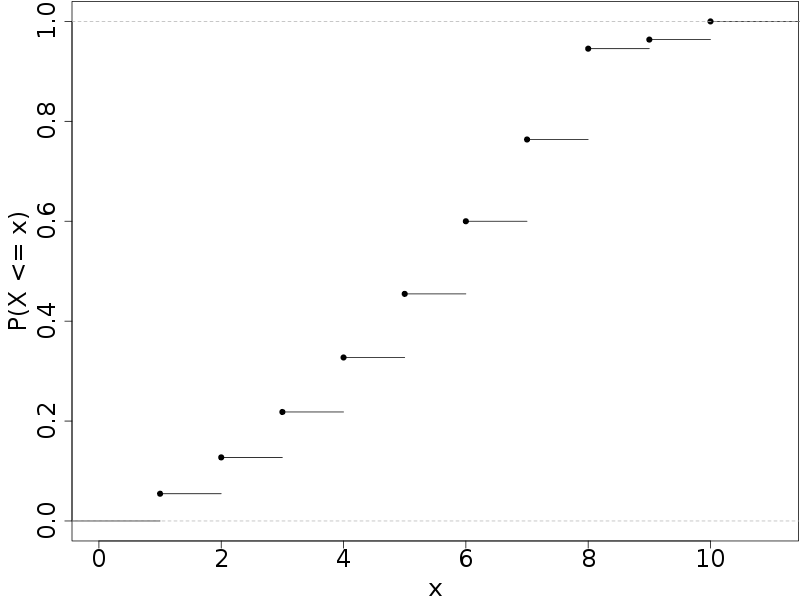
Fonction de répartition
La fonction £F_X£ définie sur £\R£ par ££\forall y \in \R, \quad F_X(y) = \P_X(]-\infty, y])££ est la fonction de répartition de la variable aléatoire £X£.
Notation : si pas d'ambiguité, £\P£ et £F£ au lieu de £\P_X£ et £F_X£.
Propriétés de la fonction de répartition
- £F(-\infty)=0£, £F(+\infty)=1£.
- £F£ est croissante : £x > y \Rightarrow F(x) \geq F(y)£.
- £F£ est continue à droite : £\lim_{y \to x+} F(y) = F(x)£.
- £\forall a,b \in \R, \quad \P(a < X \leq b) = F(b) - F(a)£.
- £F£ (en tant que fonction croissante) admet un ensemble au plus dénombrable de points de discontinuité.
Tous les points ci-dessus £-£ sauf le dernier £-£ se démontrent à partir des axiomes des probabilités.
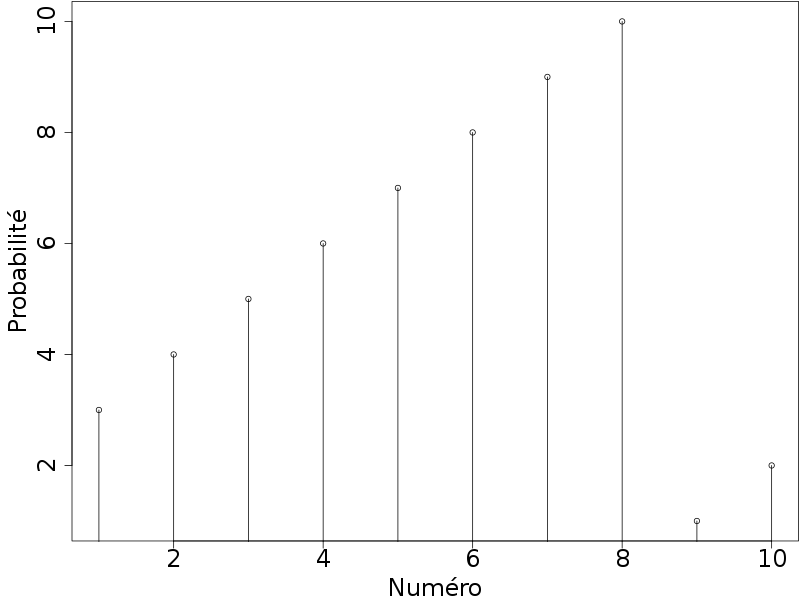
Exemple
On tire au hasard des boules numérotées de 1 à 10 dans une urne qui en contient 55, dont- 3 fois "1", 4 fois "2"
- £\dots£
- 10 fois "8"
- 1 fois "9", 2 fois "10"
£F(5) = \P(X \in \{1,\dots,5\}) = \sum_{k=1}^{5} \P(X = k) = \sum_{k=3}^{7} \frac{k}{55} = \frac{5}{11}£.
£F(8) = F(5) + \P(X \in \{6,7,8\} = \frac{5}{11} + \frac{8+9+10}{55} = \frac{52}{55}£.
Représentations graphiques
Cas particuliers
Si £X(\Omega)£ est fini ou dénombrable, £X£ définit une variable aléatoire discrète.
Si la fonction de répartition £F£ d’une VA £X£ est continue et dérivable presque partout, on dit que X est (absolument) continue, et sa dérivée £f£ est appelée densité de probabilité.
Remarque : "densité" de probabilité car ££\begin{align*} f(x) &= \lim_{h \to 0+} \frac{F(x+h) - F(x)}{h}\\ &= \lim_{h \to 0+} \frac{\P(X \in ]x, x+h])}{h} \end{align*}££
Exemples
£\Omega = \R^+£, £\cT = \cB(\R^+)£
£X(\omega \in \Omega) = \lfloor \omega \rfloor£ (partie entière)
£X(\Omega) = \N \Rightarrow£ VA discrète.
£\Omega = \cC([0,1],\R)£
£\cT = \sigma(\{t \mapsto a t + b / (a,b) \in B \times \R\}_{B \in \cB(\R^*)})£
£\Rightarrow£ VA non discrète
Propriétés
Si £f£ est une densité de probabilité, alors
- £f£ est positive : £\forall x \in \R£, £f(x) \geq 0£
- £\int_{-\infty}^{+\infty} f(t) dt = 1£
- £\int_{-\infty}^{x} f(t) dt = F(x)£
Donc £\P(a \leq X \leq b) = \int_{a}^{b} f(t) dt£
Remarque : pour une VA à densité, £\P(X = a) = 0£
Illustration
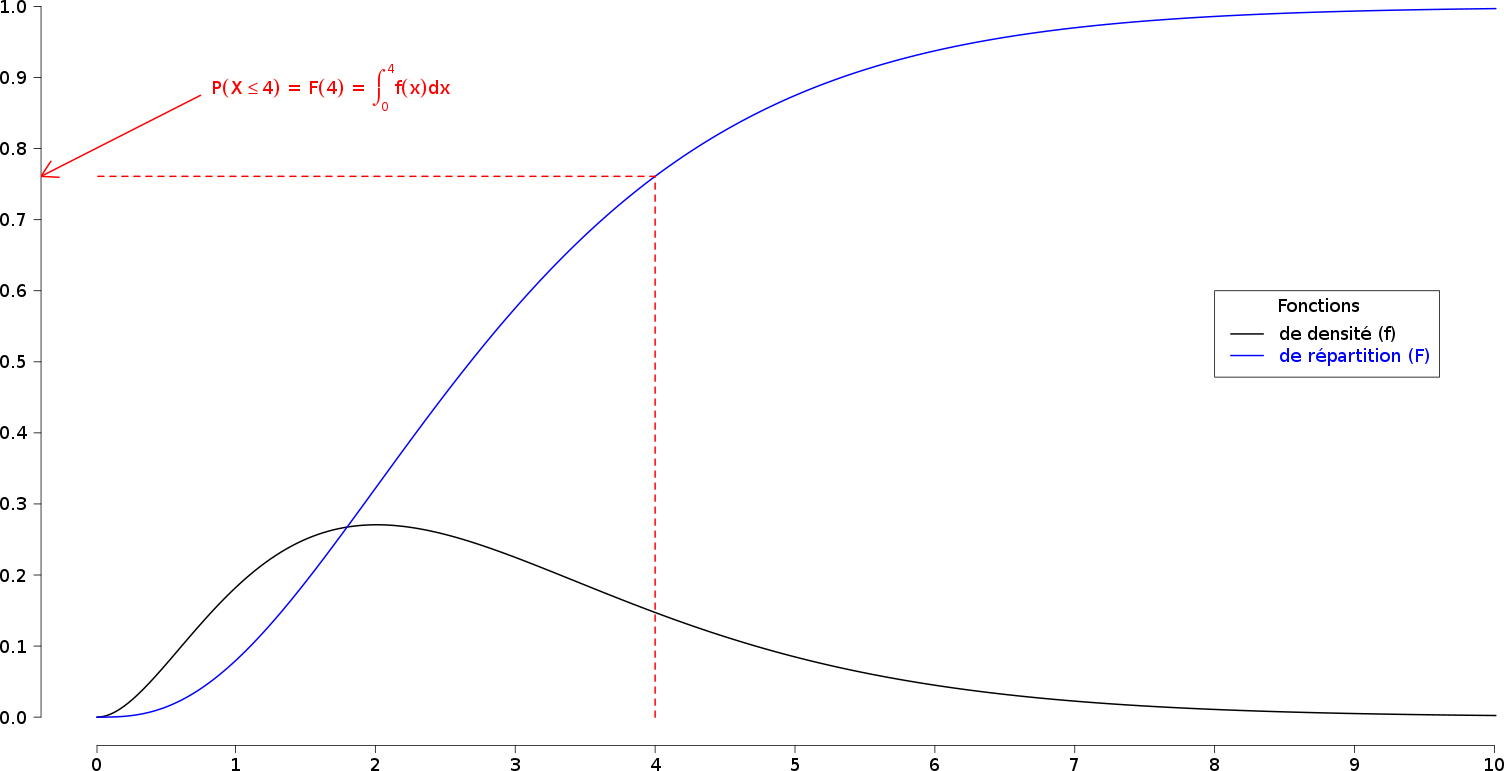
Mode, médiane, quantiles
Cas d'une VA à densité
- Mode : une abscisse £x_M£ pour laquelle la densité de probabilité présente un maximum local.
- Médiane : abscisse £x_m£ pour laquelle £F(x_m) = \frac{1}{2}£
- Quantiles d'ordre £p£ : abscisses £x_k£ pour lesquelles £F(x_k) = \frac{k}{p}£ (£1 \leq k \leq p-1£)
Pour une VA discrète c'est plus délicat (unicité ?)
Par exemple £x_k = \inf \left\{x \in \R \, / \, F(x) \geq \frac{k}{p} \right\}£
Indépendance
Des VAr. £(X_i)_{i \in I}£ sont indépendantes si pour tout sous-ensemble fini d'indices £J \subseteq I£, et pour toute famille de boréliens £(B_j)_{j \in J}£ ££\P\left(\bigcap X_j \in B_j\right) = \prod_{j \in J} \P(X_j \in B_j)££
Cela revient à dire que pour toute famille finie d'évènements £A_j = X_j^{-1}(B_j)£, £\P\left(\bigcap A_j\right) = \prod \P(A_j)£.
Remarque : les VA sont indépendantes ssi. les tribus £\{X_i^{-1}(B)\}_{B \in \cB(\R)}£ pour £i \in I£ le sont.
Critères d'indépendance
Soient £X£ et £Y£ deux VAr. définies sur le même espace probabilisé £(\Omega,\cT,\P)£. Si, pour tout £(x,y,n,m) \in \R^2 \times \N^2£
- £\P(X \leq x \cap Y \leq y) = \P(X \leq x) \times \P(Y \leq y)£, ou, si £Y(\Omega) \subseteq \N£ :
- £\P(X \leq x \cap Y = n) = \P(X \leq x) \times \P(Y = n)£, ou, si £X(\Omega) = Y(\Omega) = \N£ :
- £\P(X = n \cap Y = m) = \P(X = n) \times \P(Y = n)£,
alors X et Y sont indépendantes.
Il suffit de vérifier l'indépendance sur une classe stable par intersection finie : cf. §5 ch.6 dans Calcul des probabilités de D. Foata et A. Fuchs par exemple
Espérance, variance, moments
Dans de nombreux cas, il n'est pas nécessaire de connaître une propriété de la VA aussi précise que sa fonction de répartition. Certains paramètres numériques la caractérisant peuvent suffire. L'étude de quelques-uns de ces paramètres fait l'objet de cette sous-partie.
- Espérance = moyenne d'une VA
- Variance = dispersion autour de la moyenne
- Moments = autres descripteurs (symétrie, aplatissement...)
Intégrale par rapport à une mesure
Soit £(\Omega, \cT, \P)£ un espace probabilisé. Soit £X£ une fonction mesurable de £\Omega£ dans £\R£. On souhaite définir son intégrale par rapport à la mesure £\P£.
- Étape 1 : £\int_{\Omega} \1_A(\omega) d\P(\omega) = \P(A)£
- Étape 2 : £\int \sum_{i=1}^{n} \lambda_i \1_{A_i} d\P = \sum_{i=1}^{n} \lambda_i \P(A_i)£ (linéarité, £\lambda_i \geq 0£))
- Étape 3 : toute fonction mesurable positive £f£ est limite simple d'une suite de fonctions étagées £f_n£ et £\int f d\P = \underset{n \to +\infty}{\lim{}} \int f_n d\P£ (convergence monotone)
- Étape 4 : toute fonction mesurable s'écrit £f = f^+ - f^-£ avec £f^+(x) = \sup(0, f(x))£ et £f^-(x) = \sup(0, -f(x))£ : £\int f = \int f^+ - \int f^-£
Pour les détails, voir tout cours de théorie de la mesure / intégration niveau L3 à M1 ; celui-ci par exemple.
Espérance
On définit l'espérance d'une VAr. £X£ comme suit ££\E[X] = \int_{\Omega} X(\omega) d\P(\omega) \, ,££ sous réserve d'existence.
Exemples importants
- Si £\Omega£ est fini, £\E[X] = \sum_{\omega \in \Omega} X(\omega) \P(\omega)£
- Si £\P = \sum_{n=0}^{+\infty} \lambda_n \delta_{\omega_n}£, alors £\E[X] = \sum_{n=0}^{+\infty} \lambda_n X(\omega_n)£ (mesure discrète)
- Si £X(\Omega) = \N£, alors £\E[X] = \sum_{n=0}^{+\infty} n \P(X = n)£ (fonction étagée)
- Si £\Omega= \R£ et £\P = \mu£ mesure de Lebesgue, on reconnaît l'intégrale usuelle
Propriétés
Soient X et Y deux VAr. d'espérances finies et £\lambda \in \R£
- £\E[X + \lambda Y] = \E[X] + \lambda \E[Y]£
- £|\E[X]| \leq \E[|X|]£
- Si X et Y sont indépendantes, £\E[X \times Y] = \E[X] \times \E[Y]£
Théorème de transfert – si tout est défini
Pour toute fonction £h : \R \rightarrow \R£ mesurable, ££\E[h(X)] = \int_{\Omega} h \circ X (\omega) d\P(\omega) = \int_{\R} h(t) d\P_X(t)££ On "transfère" le calcul de l'intégrale dans l'espace £X(\Omega)£, muni de la mesure image £\P_X£
Voir par exemple §3.4 théorème 9 dans ce cours.
Espérance "usuelle"
Sous réserve de convergence...
- Si X est une VA discrète dénombrable ££E[X] = \sum_{k=1}^{+\infty} x_k \, \P(X = x_k)££
- Si X est une VA continue, £f£ étant la densité de probabilité ££E[X] = \int_{t=-\infty}^{+\infty} t \, f(t) dt££
Théorème de transfert appliqué avec £\varphi = id£
Exemples
Jeu de dés
On gagne 20€ si on obtient 4, 40€ pour le 1, mais perd 30€ sur le 6. ££X : \left\{\begin{align*} \Omega = [\negthinspace[1,6]\negthinspace] &\rightarrow \R\\ \omega \in \Omega &\mapsto 20 \delta_{4}(\omega) + 40 \delta_1(\omega) - 30 \delta_6(\omega) \end{align*}\right.££ ££\E[X] = \sum_{\omega \in \Omega} X(\omega) \P(\omega) = \frac{20}{6} + \frac{40}{6} - \frac{30}{6} = 5€££ £\Rightarrow£ On gagne en moyenne 5€ par lancer.
Loi de Cauchy
Une VA ayant pour densité £f_{a,x_0} = f£ définie par ££f(x) = \frac{1}{\pi}\frac{a}{a^2+(x-x_0)^2}££ ne possède pas d'espérance car £t \mapsto t \, f(t)£ n’est pas intégrable.
Remarques
La formule de transfert permet le constat suivant :
Il n'est pas nécessaire de déterminer la loi de probabilité de £Y = \phi(X)£ pour calculer son espérance : la connaissance de £\phi£ et de la loi de probabilité de £X£ peut suffire.
On peut toutefois expliciter la loi de £Y= \phi(X)£ dans le cas £\phi£ bijective et £X£ à densité : ££g(y) = \frac{f(\phi^{-1}(y))}{|\phi'(\phi^{-1}(y))|}££ C.f. polycopié du cours.
Exemple : £Y = \phi(X)£
Quand £\phi£ n'est pas bijective, il faut rechercher un antécédent pour £X£ de l'évènement "£Y \leq y£".
Cas £Y = X^2£
Soit £y > 0£. £Y \leq y \Leftrightarrow |X| \leq \sqrt{y}£. Donc ££\begin{align*} G(y) &= \P(Y \leq y)\\ &= \P(-\sqrt{y} \leq X \leq \sqrt{y})\\ &= F(\sqrt{y}) - F(-\sqrt{y}) \end{align*}££ Finalement, £g(y) = \frac{1}{2 \sqrt{y}} \left( f(\sqrt{y}) + f(-\sqrt{y}) \right)£.
Moments
Étant données une VA £X£ d'espérance finie, on appelle variable aléatoire centrée la VA ££Y = X − \E[X]££
On appelle moment d'ordre £s \in \N^*£ d'une VA £X£ la quantité – sous réserve d'existence ££m_s(X) = \E[X^s]££
Moment centré d'ordre £s£ : ££\mu_s(X) = \E[(X - \E[X])^s]££
Dispersion d'une VA
Variance d'une VAr. = moment centré d'ordre 2.
££\mbox{Var(X)} = \mu_2(X) = \E[(X − \E[X])^2] \geq 0££
Écart-type = racine carrée de la variance. ££\sigma(X) = \sqrt{\mbox{Var}(X)}££
La variance (comme l'écart-type) est une mesure de la dispersion (nom parfois donné à la variance) des valeurs de la VA autour de son espérance
Illustration
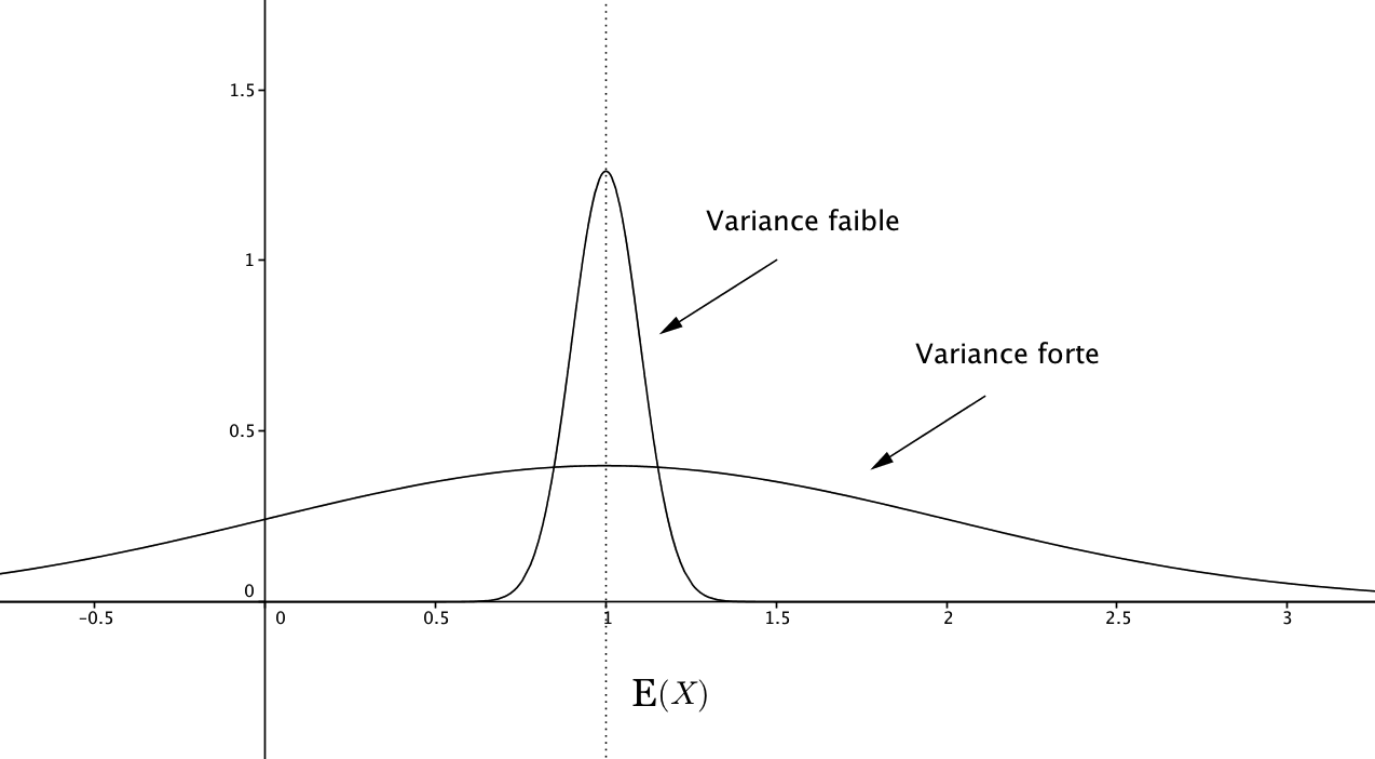
Propriétés
- La variance est toujours positive : £\mbox{Var}(X) \geq 0£
- Pour tous £a, b \in \R£, £\mbox{Var}(aX + b) = a^2 \mbox{Var}(X)£
- £\mbox{Var}(X) = \E[X^2] - \E[X]^2£
- Si £X_1£ et £X_2£ sont deux VA indépendantes, £\mbox{Var}(X_1 + X_2) = \mbox{Var}(X_1) + \mbox{Var}(X_2)£
Démonstration : définition + £\E[X_1 \times X_2] = \E[X_1] \times \E[X_2]£ si indépendance
Exemple
Soit une VA £X£ ayant pour densité £f(t) = \left\{ \begin{align*} &t/2 \mbox{ si } 0 \leq t < 2\\ &0 \mbox{ sinon} \end{align*} \right. £
Alors £\int_0^2 f(t) dt = \left[ \frac{x^2}{4} \right]_0^2 = 1£, et ££\E[X] = \int_0^2 t \, f(t) dt = \left[ \frac{t^3}{6} \right]_0^2 = \frac{4}{3}££ ££\begin{align*}\mbox{Var}(X) &= \E[X^2] - \E[X]^2\\ &= \int_0^2 t^2 \, f(t) dt - \left(\frac{4}{3}\right)^2\\ &= \left[ \frac{x^4}{8} \right]_0^2 - \frac{16}{9} = \frac{2}{9} \end{align*}££
Propositions
Inégalité de Markov
Soit £X£ une VAr. intégrable ££\forall x > 0, \,\, \P(|X| \geq x) \leq \frac{\E[|X|]}{x}££ Preuve : ²X \geq x \1_{X \geq x}, \dots²
Corollaire
Soient ²\phi² une fonction croissante d'un intervalle ²I² dans ²\R^+², et ²X² une VAr. telle que ²\P(X \in I) = 1² ²²\forall x \in I \, / \, \phi(x) > 0 \, , \quad \P(X \geq x) \leq \frac{\E[\phi(X)]}{\phi(x)}²²
Inégalité de Bienaymé-Tchebyshev
Soit £X£ une VAr. admettant un moment d'ordre 2. ££\forall x > 0, \,\, \P(|X - \E[X]| \geq x) \leq \frac{\mbox{Var}(X)}{x^2}££
Preuve : ²²\begin{align*} \P(|X - \E[X]| \geq x) &= \int_{\frac{(X - \E[X])^2}{x^2} \geq 1} 1 d\P\\ &\leq \int_{\frac{(X - \E[X])^2}{x^2} \geq 1} \frac{(X - \E[X])^2}{x^2} d\P\\ &\leq \frac{1}{x^2} \int_{\Omega} (X - \E[X])^2 d\P \end{align*}²²
Lois de probabilités usuelles
Lois discrètes
Loi uniforme
Distribution qui véhicule le moins d'information (entropie maximale)
£\begin{align*}& \quad X(\Omega) = [\negthinspace[ 1,n ]\negthinspace]\\ &\quad \P(X = k) = \frac{1}{n}\end{align*}£
Notation : £X \sim \cU([\negthinspace[ 1,n ]\negthinspace])£ ou £X \sim \cU(n)£
Loi uniforme discrète (suite)
££\E[X] = \frac{n+1}{2} \, , \quad \mbox{Var}(X) = \frac{n^2-1}{12}££
Exemple : £X \sim \cU[\negthinspace[0,255]\negthinspace]£.
En chaque point £(i, j) \in [\negthinspace[1, 100]\negthinspace]^2£, on représente une réalisation £X(\omega)£ en niveaux de gris.

Loi de Bernoulli
C'est la loi d'une VA £X£ ne pouvant prendre que les deux valeurs 1 ou 0 avec les probabilités £p£ et £1 - p£.
££\left\{ \begin{align*} X(\Omega) &= \{0, 1\}\\ \P(X = 1) &= p\\ \P(X = 0) &= 1-p = q \end{align*} \right.££
On pourra noter £X \sim Ber(p)£ (non standard)
££\E[X] = p \, , \quad \mbox{Var}(X) = pq££
Inégalité de Hoeffding
Soit ²(X_n)² une suite de VA indépendantes à support dans ²[a,b]²
²²\P(\overline{X_n} - \E[\overline{X_n}] \geq \varepsilon) \leq \exp\left(-\frac{2 n \varepsilon^2}{(b-a)^2}\right) \geq \P(\overline{X_n} - \E[\overline{X_n}] \leq -\varepsilon) \, ,²²
avec ²\overline{X_n} = \frac{1}{n} \sum_{k=1}^{n} X_k².
Application : ²X_n \sim Ber(p)²
Bienaymé-Tchebyshev :
²\P\left(|\overline{X_n} - p| \geq \frac{x}{\sqrt{n}}\right) \leq \frac{p(1-p)}{x^2}²
Hoeffding :
²\P\left(|\overline{X_n} - p| \geq \frac{x}{\sqrt{n}}\right) \leq 2 \exp(-2 x^2)²
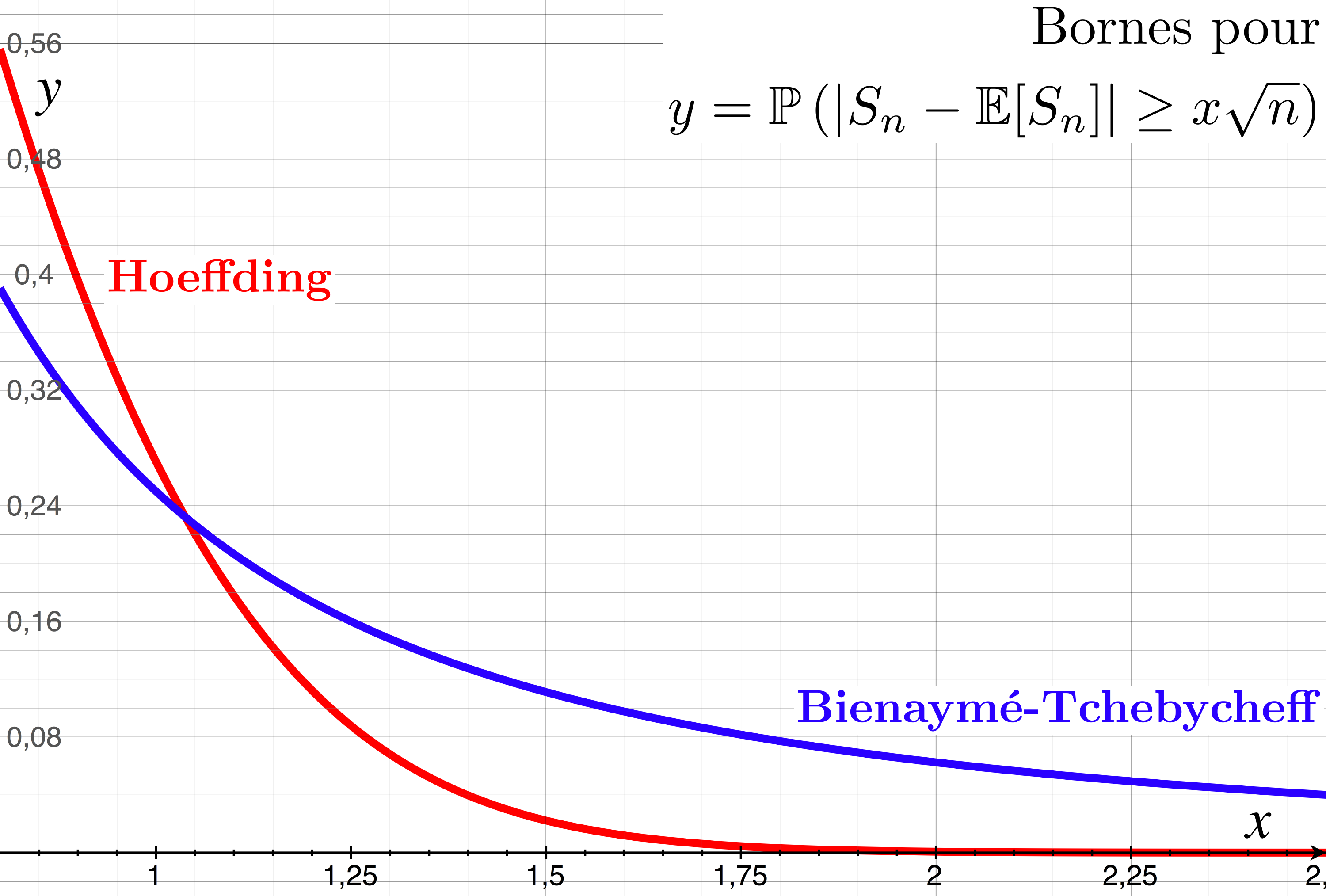
Loi binomiale
Soient £n \in \N^*£ et £p \in [0, 1]£. Une VA £X£ suit la loi binomiale de paramètres £n£ et £p£ notée £\cB(n, p)£ si ££\left\{ \begin{align*} X(\Omega) &= [\negthinspace[ 0, n ]\negthinspace]\\ \P(X=k) &= C_n^k p^k (1-p)^{n-k} \end{align*} \right. ££
On modélise ainsi le cas où une même expérience aléatoire est répétée plusieurs fois. Plus précisément £X£ est la somme de £n£ VA de Bernouilli indépendantes de paramètre £p£.
££\E[X] = np \, , \quad \mbox{Var}(X) = npq££
Illustration
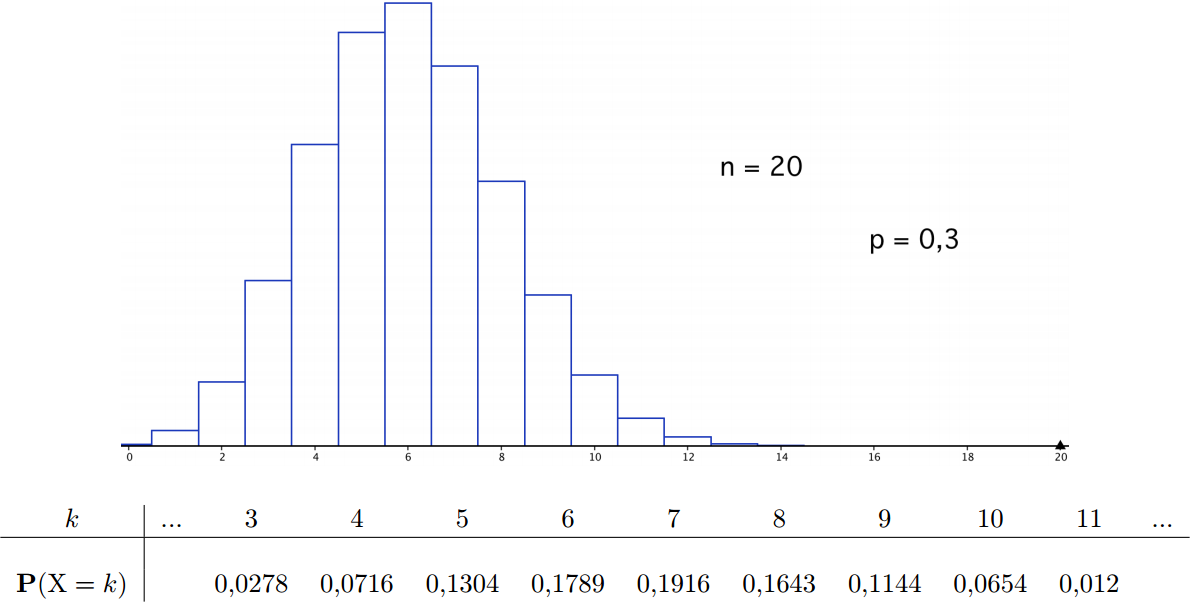
Loi de Poisson
Soit £\lambda£ un réel positif. On dit que £X£ suit la loi de Poisson £\cP(\lambda)£ si ££ \left\{ \begin{align*} X(\Omega) &= \N\\ \P(X = k) &= e^{-\lambda} \frac{\lambda^k}{k!} \end{align*} \right. ££
La loi de Poisson modélise par exemple le nombre d’appels à un central téléphonique pendant une période donnée, le nombre de voitures qui passent à un carrefour en un temps donné...
££\E[X] = \lambda \, , \quad \mbox{Var}(X) = \lambda££
Exemple / exercice
Un central téléphonique reçoit en moyenne 100 appels par heure. En supposant que le nombre d'appels durant un intervalle de temps quelconque suit une loi de Poisson,
- quelle est la probabilité que le central reçoive trois appels en deux minutes ?
- quelle est la probabilité pour qu'en deux minutes, il reçoive au moins un appel ?
- 100 appels par heure £\Rightarrow£ en moyenne £\frac{100}{30}£ en 2 minutes. £X \sim \cP(10/3)£.
£\P(X = 3) = e^{-3} \frac{10^3}{6 \times 3^3} \simeq 0.220£ - £\P(\mbox{"au moins un appel"}) = 1 - \P(\mbox{"aucun appel"}) = 1 - e^{-10/3} \simeq 0.964£
Loi géométrique
Pour £p \in [0, 1]£, on définit la loi géométrique £\cG(p)£ par ££ \left\{ \begin{align*} X(\Omega) &= \N^*\\ \P(X = k) &= (1-p)^{k-1} p = q^{k-1} p \end{align*} \right. ££
£\P(X = k)£ = probabilité d'obtenir au cours de £k£ épreuves de Bernouilli indépendantes, £k-1£ échecs suivis d'un succès.
££\E[X] = \frac{1}{p} \, , \quad \mbox{Var}(X) = \frac{q}{p^2}££
Loi hypergéométrique
Soient £p \in [0, 1]£, £n \in \N£ et £A \in [\negthinspace[n, +\infty]\negthinspace]£. £X£ suit la loi hypergéométrique £\cH(n, p, A)£ si ££ \left\{ \begin{align*} X(\Omega) &\subseteq [\negthinspace[0,n]\negthinspace]\\ \P(X = k) &= \frac{\binom{pA}{k} \, \binom{qA}{n-k}}{\binom{A}{n}} \end{align*} \right. ££
Exemple / explication :
On tire n boules (sans remise) dans une urne contenant £pA£ boules rouges et £qA£
boules bleues, soit un nombre total de boules de £A = pA + qA£. Alors la VA donnant
le nombre de boules rouges suit une loi £\cH(n, p, A)£.
££\E[X] = np \, , \quad \mbox{Var}(X) = npq \frac{A - n}{A - 1}££
Lois continues
Loi uniforme
£X£ suit la loi uniforme sur £[a, b]£ si ££ \left\{ \begin{align*} X(\Omega) &= [a,b]\\ f(x) &= \frac{1}{b-a} \1_{[a,b]}(x) \end{align*} \right. ££
On note £X \sim \cU([a,b])£ ou £X \sim \cU(a,b)£.
££\E[X] = \frac{a+b}{2} \, , \quad \mbox{Var}(X) = \frac{(b-a)^2}{12}££
Loi exponentielle
£X£ suit la loi exponentielle de paramètre £\lambda£, notée £\cT(\lambda)£, si ££ \left\{ \begin{align*} X(\Omega) &= \R^+\\ f_{\lambda}(x) &= \lambda e^{-\lambda x} \1_{\R^+}(x) \end{align*} \right. ££
La loi exponentielle intervient dans les processus continus sans mémoire comme la désintégration d'un noyau atomique, l'émission d’un électron... Elle généralise au cas continu la loi géométrique.
££\E[X] = \frac{1}{\lambda} \, , \quad \mbox{Var}(X) = \frac{1}{\lambda^2}££
Loi normale (de Laplace-Gauss)
£X£ suit la loi normale de paramètre £(\mu, \sigma)£, notée £\cN(\mu, \sigma)£, si ££ \left\{ \begin{align*} X(\Omega) &= \R\\ f_{\mu, \sigma}(t) &= \frac{1}{\sigma \sqrt{2 \pi}} \exp \left( -\frac{(x - \mu)^2}{2 \sigma^2} \right) \end{align*} \right. ££
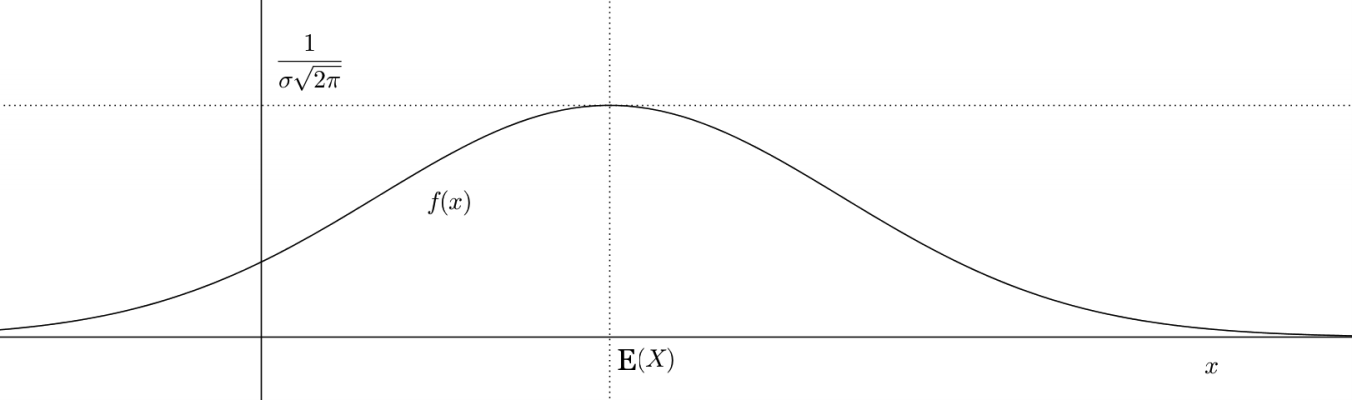
Loi normale (suite)
££\E[X] = \mu \, , \quad \mbox{Var}(X) = \sigma^2££ (Changements de variables : cf. poly)
Proposition
Si £X£ suit une loi normale £\cN(0, 1)£, alors pour £\sigma \neq 0£, la VA £Y = \sigma X + \mu£ suit la loi normale £\cN(\mu, \sigma)£.
Plus généralement, toute transformation affine d'une loi normale est encore une loi normale.
Remarque : les calculs pratiques nécessitent des tables
Rappel
La fonction Gamma est définie sur £[1, +\infty[£ par ££\Gamma : z \mapsto \int_{0}^{+\infty} t^{z-1} e^{-t} dt££
C'est un prolongement de la factorielle. On a par exemple les relations ££\forall n \in \N, \, \Gamma(n + 1) = n! \mbox{ et } \Gamma\left(\frac{1}{2}\right) = \sqrt{\pi}££
Voir par exemple la page Wikipedia
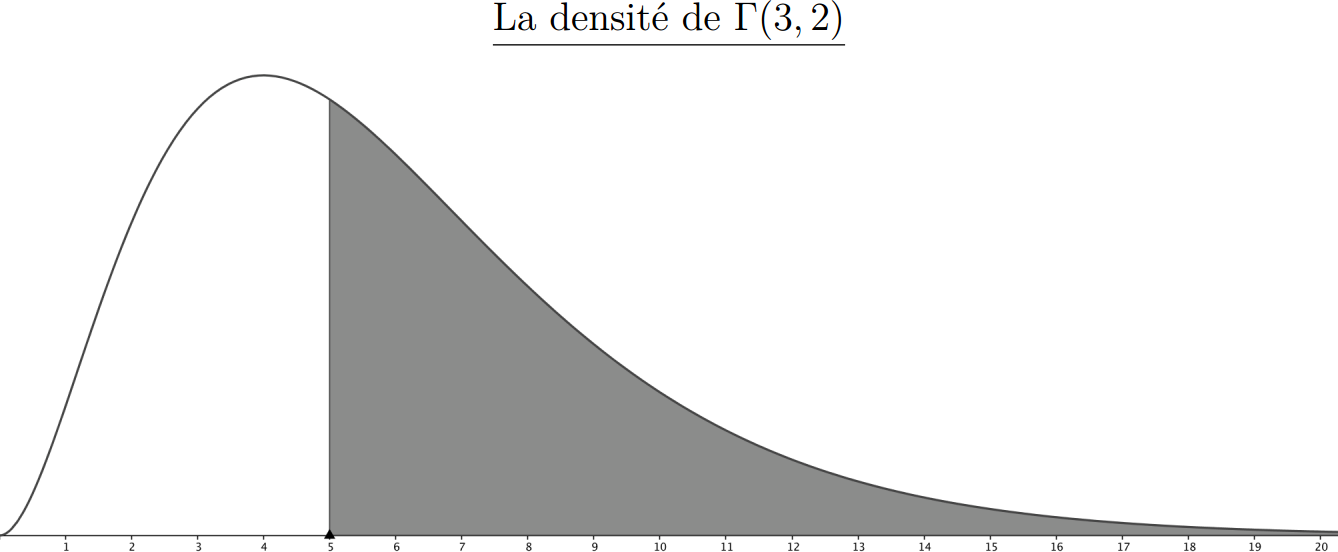
Loi Gamma
£X£ suit la loi Gamma de paramètre £(\alpha, \beta)£, notée £\Gamma(\alpha, \beta)£, si ££ \left\{ \begin{align*} X(\Omega) &= \R^+\\ f_{\alpha, \beta}(t) &= t^{\alpha-1} \frac{\beta^{\alpha} e^{-\beta t}}{\Gamma(\alpha)} \end{align*} \right. ££
La loi Gamma généralise la loi exponentielle (obtenue pour £\alpha=1£).
££\E[X] = \frac{\alpha}{\beta} \, , \quad \mbox{Var}(X) = \frac{\alpha}{\beta^2}££
Illustration
Loi du £\chi^2£
£X£ suit la loi du £\chi^2£ ("khi-deux") à £k£ degré(s) de liberté si ££ \left\{ \begin{align*} X(\Omega) &= \R^+\\ f_k(t) &= \frac{1}{2^{k/2} \Gamma(k/2)} t^{\frac{k}{2} - 1} e^{-\frac{t}{2}} \end{align*} \right. ££
La loi du £\chi^2£ est très classique en statistiques. Le test du £\chi^2£ permet de savoir si un échantillon donné est en adéquation avec une loi de probabilité donnée.
££\E[X] = k \, , \quad \mbox{Var}(X) = 2k££
Exemples
On reprend la recherche de la loi de £Y = X^2£ :
£g(y) = \frac{1}{2 \sqrt{y}} (f(\sqrt{y}) + f(-\sqrt{y}))£
Si £X£ suit la loi £\cN(0, 1)£, alors ££g(y) = \frac{1}{\sqrt{2 \pi y}} e^{-\frac{y}{2}}££ On reconnaît la loi du £\chi^2£ à 1 degré de liberté
Plus généralement,
La somme des carrés de £k£ lois normales centrées réduites indépendantes suit une loi du £\chi^2£ à £k£ degré(s) de liberté.
Beaucoup d'autres lois...
- Loi de Zipf
- Loi binomiale négative
- Loi bêta
- Loi de Pareto
- Loi de Weibull
- Loi £t£ de Student
- ... etc
Et diverses lois multivariées...
Voir par exemple la page Wikipedia.
Convolution, loi d'une somme
Un problème courant consiste à trouver la loi de probabilité d'une somme de deux VA indépendantes : ££Z = X + Y££
Les méthodes de calcul font en général apparaître un produit de convolution
Cas discret
Théorème des probabilités totales : ££\begin{align*} \P(Z = z) &= \sum_{x, y \in X(\Omega) \times Y(\Omega)} \P(X+Y = z \cap X = x)\\ &= \sum_{x \in X(\Omega)} \P(X = x \cap Y = z - x)\\ &= \sum_{x \in X(\Omega)} \P(X = x) \times \P(Y = z-x) \mbox{ si indépendance } \end{align*} ££
Remarque : certains termes peuvent être nuls. £x£ (resp. £y£) ne prend pas nécessairement toutes les valeurs possibles de £X£ (resp. £Y£), mais uniquement celles compatibles avec l'évènement £Z = z£.
Propositions
La somme de deux VA indépendantes de lois de Poisson £\cP(\lambda)£ et £\cP(\mu)£ suit la loi de Poisson £\cP(\lambda + \mu)£.
La somme de deux VA indépendantes de lois binomiales £\cB(n, p)£ et £\cB(m, p)£ suit une loi binomiale £\cB(n+m, p)£.
Exercices ou cf. poly de cours
Cas continu
Rappel : sous réserve de convergence, on définit le produit de convolution ££(f * g)(x) = \int_{\R} f(x-y) g(y) dy££
La densité de probabilité de la somme de deux VA à densité indépendantes est le produit de convolution des densités des deux VA. ££f_{X+Y} = f_X * f_Y££
Remarque : traduction "continue" de la formule discrète
Propositions
La somme de deux lois Gamma indépendantes £\Gamma(r, \lambda)£ et £\Gamma(s, \lambda)£ suit la loi Gamma £\Gamma(r + s, \lambda)£.
La somme de deux lois normales indépendantes £\cN(\mu, \sigma)£ et £\cN(\mu', \sigma')£ suit la loi normale £\cN(\mu + \mu', \sqrt{\sigma^2 + \sigma'^2})£.
Exercices ou cf. poly de cours
/