£ \newcommand{\cC}{{\cal C}} \newcommand{\cT}{{\cal T}} \newcommand{\cE}{{\cal E}} \newcommand{\cP}{{\cal P}} \newcommand{\cB}{{\cal B}} \newcommand{\cU}{{\cal U}} \newcommand{\cA}{{\cal A}} \newcommand{\cL}{{\cal L}} \newcommand{\cG}{{\cal G}} \newcommand{\cH}{{\cal H}} \newcommand{\cS}{{\cal S}} \newcommand{\cN}{{\cal N}} \newcommand{\cD}{{\cal D}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\E}{\mathrm{E}} \newcommand{\R}{\mathbb{R}} \newcommand{\P}{\mathrm{P}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\U}{\mathbb{U}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\L}{\mathbb{L}} \newcommand{\1}{\mathbb{1}} \newcommand{\puiss}{e\thinspace \mbox{\small -}} \newcommand{\esp}{\thinspace} \newcommand{\tr}{{}^t \negthinspace} £

Vecteurs aléatoires et simulation

Introduction

Aiguilles de Buffon

Expérience :
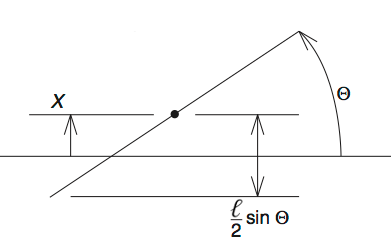
On jette ²n² aiguilles toutes de même longueur ²\ell \leq L² sur un parquet dont les lames sont de largeur ²L².

Paramétrisation : VAr.

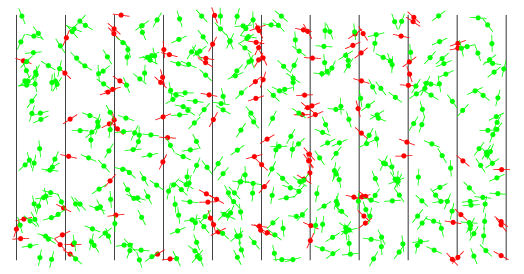
²X \sim \cU([0,L/2])² = distance du centre à la lame la plus proche
²\Theta \sim \cU([0,\pi/2])² = angle aigu formé avec la lame

Aiguilles de Buffon - suite

²I² = "Intersecter une lame" : ²\frac{\ell}{2} \sin{\Theta} \geq X², donc ²²\begin{align*}\P(I) &= \frac{4}{\pi L} \int_{\left[0, \frac{\pi}{2}\right] \times \left[0,\frac{L}{2}\right]} \1_{\frac{\ell}{2} \sin{\theta} \geq x} d\theta dx\\ &= \frac{4}{\pi L} \int_{\theta=0}^{\frac{\pi}{2}} \int_{x=0}^{\frac{\ell}{2} \sin{\theta}} 1 d\theta dx\\ &= \frac{2 \ell}{\pi L} \int_{0}^{\frac{\pi}{2}} \sin{\theta} d\theta = \frac{2 \ell}{\pi L} \end{align*}²²

Loi des grands nombres ²\Rightarrow² estimation de ²\pi²

(Attention : convergence très lente...)

Couples de VAr.

Soient ²X² et ²Y² deux VAr. définies sur un même espace probabilisé ²(\Omega, \cT, \P)².
À chaque évènement élémentaire ²\omega² on associe le couple ²(X(\omega), Y(\omega)) \in \R^2²

Note : ²(X, Y)² est encore une variable aléatoire, mais à valeurs dans ²\R^2².
On peut en fait définir des VA sur tout espace mesuré.

Figure : ²²\{ (X-0.5)^2 + Y^2 \leq 1 \} \bigcap \{ X^2 + (Y-0.5)^2 \leq 1 \}²²

On a ainsi défini un couple ²(X, Y)² de variables aléatoires réelles, aussi appelé vecteur aléatoire (de dimension 2).

Lois jointes et lois marginales

Définition

Soient ²X² et ²Y² deux VAr. définies sur un même espace probabilisé ²(\Omega, \cT, \P)².
Fonction de répartition conjointe de ²X² et ²Y² (ou f. de r. du couple ²(X, Y)²) : ²²F_{X,Y}(x, y) = \P(X \leq x \cap Y \leq y)²²

Définition

Fonctions de répartition marginales de ²X² et ²Y², notées ²F_X² et ²F_Y² : ²²F_X(x) = \lim_{y \to +\infty} F_{X,Y}(x, y) = \P(X \leq x)²² ²²F_Y(y) = \lim_{x \to +\infty} F_{X,Y}(x, y) = \P(Y \leq y)²²

Notation : si pas d'ambiguité on écrit juste ²F(x,y)² et ²F(x)², ²F(y²)

Indépendance

Deux VAr. ²X² et ²Y² sont indépendantes ssi. ²²\forall x,y \in \R \, , \quad F(x,y) = F(x) \times F(y)²² (Réécriture de la caractérisation déjà vue)

L'objet de cette séance est d'étudier le cas des variables "liées".

On commence par définir la notion de probabilité ponctuelle d'un couple dans le cas discret, et de fonction de densité d'un couple dans le cas continu.

Loi jointe : cas discret

Si ²X² et ²Y² prennent des valeurs ²x_i² et ²y_j² en nombre fini ou dénombrable, la loi jointe du couple ²(X, Y)², notée ²P_{X,Y}², est entièrement définie par les ²²\P_{X,Y}(x_i, y_j) = \P(X = x_i \text{ et } Y = y_j)²² On note ²p_{i,j} = \P_{X,Y}(x_i, y_j)².

Les probabilités d'un couple discret à valeurs finies se résument dans un tableau :

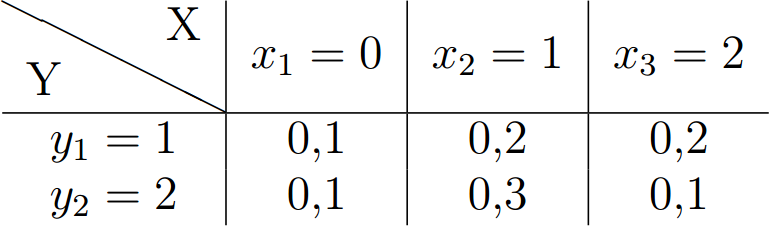
Lois marginales

Lois de ²X² et ²Y² prises séparément

Loi marginale de ²X² : ²\P(X = x_i) = \sum_{j} p_{i,j} := p_i²
Loi marginale de ²Y² : ²\P(Y = y_j) = \sum_{i} p_{i,j} := p^{(j)}²

On lit ces probabilités dans les "marges" du tableau :

Exemple / Exercice

(dans le poly de cours de l'ENSIMAG)
Une urne contient ²r² boules dont ²r_1² sont blanches et ²r_2² sont noires. On effectue ²n² tirages successifs avec remise. À l'issue des ²n² tirages, on note ²X² (resp. ²Y²) le nombre de boules blanches (resp. noires).

Déterminer la loi du couple ²(X, Y)² et les lois (marginales) de ²X² et ²Y².

Solution

Pour ²k,\ell \in \N \, / \, k+\ell = n², ²²\P(X=k \text{ et } Y=\ell) = \frac{(k+\ell)!}{k! \, \ell!} p_1^k p_2^{\ell}²² avec ²p_1 = \frac{r_1}{r}² et ²p_2 = \frac{r_2}{r}².

Les lois marginales sont ²\cB(n, p_1)² et ²\cB(n, p_2)²

Couple discret de VAs indépendantes

Deux VAs discrètes X et Y sont indépendantes ssi. ²²\forall (i,j) \, \, \P(X = x_i \cap Y = y_j) = p_i \, p^{(j)}²²

Si on garde les lois marginales trouvée sur l'exemple, le tableau des probabilités s'écrit :

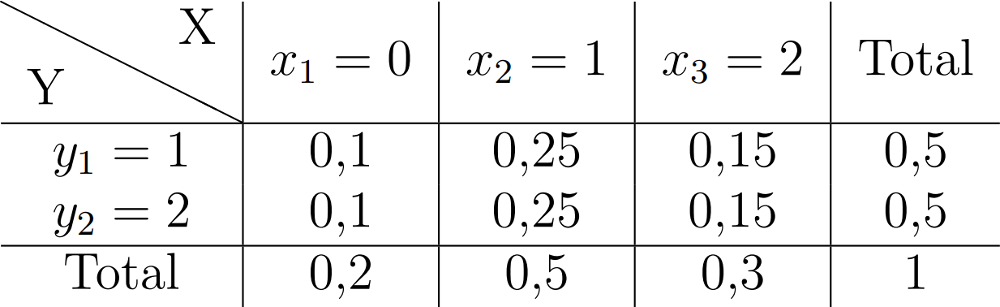
Densité d'un couple

Soit un couple de VAs ²(X,Y)² de fonction de répartition conjointe ²F_{X,Y}². Si ²F² est ²\cC^2² on définit la densité du couple ²(X,Y)² notée ²f_{X,Y}² par ²²f_{X,Y} = \frac{\partial^2 F_{X,Y}}{\partial x \partial y}²² As usual : notations ²F² et ²f² si pas d'ambiguité.

Ainsi, ²²F(x,y) = \int_{u=-\infty}^{x} \int_{v=-\infty}^{y} f(u,v) \, du \, dv²²

Calculs de probabilités

²²\P(X \leq x \cap Y \leq y) = \int_{u=-\infty}^{x} \int_{v=-\infty}^{y} f(u,v) du dv = F(x,y)²² ²²\P(X \in ]a,b] \, \cap \, Y \in ]c,d]) = F(b,d) - F(a,c)²² Plus généralement : ²²\forall A \in \cB(\R^2) \, , \, \P((X,Y) \in A) = \int_{(u,v) \in A} f(u,v) \, du \, dv²²

Les fonctions de répartition marginales sont définies par ²²F_X(x) = \int_{u=-\infty}^{x}\int_{v=-\infty}^{+\infty} f(u,v) \, du \, dv = \P(X \leq x)²² ²²F_Y(y) = \int_{u=-\infty}^{+\infty}\int_{v=-\infty}^{y} f(u,v) \, du \, dv = \P(Y \leq y)²²

Exemple de calcul

²X² VAr. de loi exponentielle ²\cE(1)²
²Y² VAr. de loi uniforme ²\cU(0,2)²
Indépendance supposée (²\Leftrightarrow f_{X,Y} = f_X f_Y²)

²²\begin{align*} \P((X,Y) \in [0,1]^2) &= \int_{x=0}^{1} \int_{y=0}^{1} \frac{e^{-x}}{2} dx dy\\ &= \int_{x=0}^{1} \frac{e^{-x}}{2} dx\\ &= \frac{1}{2} (1 - e^{-1}) \end{align*}²²

Changement de variables

Soient ²U², ²V² deux ouverts bornés de ²\R^n², ²\psi : U \rightarrow V² un difféomorphisme de classe ²\cC^1², et ²f² une application de ²V² dans ²\R². Alors (si tout est intégrable) ²²\int_V f(y) dy = \int_U f(\psi(x)) |D(\psi)(x)| \, dx²²

²D(\psi)(x) = det\left(\frac{\partial \psi_i}{\partial x_j}\right)²

Exemple : passage en coordonnées polaires, ²\psi : (r,\theta) \mapsto (r \cos \theta, r \sin \theta)², ²|D(\psi)(r,\theta)| = r² et ²²\int_{\cD(\rho)} f(x) dx = \int_{\theta=-\pi}^{\pi} \int_{r=0}^{\rho} f(r \cos \theta, r\sin\theta) r \, dr \, d\theta \, ,²² où ²\cD(\rho)² = disque centré de rayon ²\rho².

Covariance et coefficient de corrélation

Les définitions introduites au chapitre précédent sur les moments d’une variable aléatoire peuvent être étendues à ²d² variables aléatoires définies sur un même espace probabilisé ²(\Omega, \cT, \P)².

Dans la pratique, on utilise essentiellement les moments du premier ordre, et les moments centrés du second ordre.

²²V = \begin{pmatrix} X_1\\ \vdots\\ X_d \end{pmatrix}²²

Espérance : ²\E[V] = \begin{pmatrix} \mu_1 = E[X_1]\\ \vdots\\ \mu_d = \E[X_d] \end{pmatrix}²

Covariance : matrice de terme général ²²\Sigma_{i,j} = \text{Cov}(X_i, X_j) = \E[(X_i - \E[X_i])(X_j - \E[X_j])]²² Remarque : ²\text{Cov}(X_i, X_i) = \text{Var}(X_i)²

Propriétés de la covariance

Bilinéarité

²²\text{Cov}\left(\sum_i \lambda_i X_i, \sum_j \mu_j Y_j\right) = \sum_{i,j} \lambda_i \mu_j \text{Cov}(X_i, Y_j)²²

Corollaire

²²\text{Var}\left(\sum_i^{n} \alpha_i X_i\right) = \sum_i^{n} \alpha_i^2 \text{Var}(X_i) + 2 \sum_{1 \leq i < j \leq n} \alpha_i \alpha_j \text{Cov}(X_i, X_j)²²

Preuve : écrire les définitions.

La covariance

Généralisation

On peut définir des couples de VAr. ni discrets ni à densité. Par exemple ²X \sim \cP(\lambda)² et ²Y \sim \cN(\mu, \sigma)². On écrit alors ²²\P(X = k \text{ et } Y \in I) = \P(X^{-1}(\{k\}) \cap Y^{-1}(I))²²

Il faut alors faire attention en calculant l'espérance relativement à la loi du couple : ²²\text{Cov}(X,Y) = \int_{\omega \in \Omega} (X(\omega) - \E[X]) (Y(\omega) - \E[Y]) d\P(\omega)²² Sur l'exemple ci-dessus : ²²\text{Cov}(X,Y) = \sum_{n=1}^{+\infty} \left(n - \frac{1}{\lambda} \right) e^{-\lambda} \frac{\lambda^n}{n!} \int_{x = -\infty}^{+\infty} (x - \mu) \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} dx²²

Preuve de l'inégalité de Cauchy-Schwarz

On considère le polynôme ²²P(t) = || t u + v ||^2 = \langle t u + v, t u + v \rangle = t^2 ||u||^2 + 2 t \langle u, v \rangle + ||v||^2 ²² Il est toujours positif, donc son discriminant est négatif ou nul : ²²4 \langle u, v \rangle^2 - 4 ||u||^2 ||v||^2 \leq 0²² On aboutit à l'inégalité souhaitée.

Note : il existe une démonstration géométrique ; on peut aussi directement calculer ²\left|\left| \frac{u}{||u||} \pm \frac{v}{||v||} \right|\right|^2². Voir par exemple ce document.

Exemple de calcul

²X \sim \cE(2)² et ²Y = 1 - 2X²
²\E[X] = \frac{1}{2}² et ²\E[Y] = 0²

²²\begin{align*} \P(X \leq x \text{ et } Y \leq y) &= \P\left(X \leq x \text{ et } X \geq \frac{1 - y}{2}\right)\\ &= \1_{2x \leq 1-y} (e^{-x} - e^{-\frac{1-y}{2}}) \end{align*}²² Non dérivable sur la droite ²2x = 1 - y², donc pas de densité.

²²\begin{align*} \text{Cov}(X,Y) &= \E[XY] - \E[X]\E[Y]\\ &= \int_{0}^{+\infty} 2 (x - 2 x^2) e^{-2x} dx - 0\\ &= \E[X] - 4 \int_{0}^{+\infty} x^2 e^{-2x} dx\\ &= \E[X] - 2\E[X] = -\frac{1}{2} \end{align*}²²

Vecteurs gaussiens

Définition

Un vecteur de VAr. ²(X_1, \dots, X_d)² est dit gaussien si toute combinaison linéaire non nulle de ses coordonnées est une VAr. normale.

Expression de la densité : ²²f_{X_1,\dots,X_d}(x \in \R^d) = \frac{1}{(2 \pi)^{d/2} |\Sigma|^{1/2}} e^{-\frac{1}{2} (x - \mu)^{T} \Sigma^{-1} (x - \mu)}²²

Propriété : si deux composantes ²X_i² et ²X_j² sont décorrélées (²\rho_{i,j} = 0²), alors elles sont indépendantes.

Preuve : on écrit la fonction caractéristique ²\varphi(u) = \E[e^{i\langle u,X\rangle}]² qui se factorise en le produit des fonctions caractéristiques des composantes ²X_i². Cf. par exemple p.8 dans ce document

Lois conditionnelles (VA à densité)

Si ²X² et ²Y² sont dépendantes, on écrit ²²\begin{align*} \P(Y \leq y \, | X \in [a, b]) &= \frac{\P(X \in [a,b] \text{ et } Y \leq y)}{\P(X \in [a,b])}\\ &= \frac{\int_{a}^{b} \int_{-\infty}^{y} f(u,v) du \, dv}{\int_{a}^{b} \int_{-\infty}^{+\infty} f(u,v) du \, dv} \end{align*}²²

Fonction de répartition conditionnelle

²²F(y|x) = \lim_{a,b \to x} \P(Y \leq y \, | X \in [a, b]) = \frac{1}{f_X(x)} \int_{-\infty}^{y} f(x,v) dv²²

Densité de probabilité conditionnelle

²²f(y|x) = \frac{\partial F(y|x)}{\partial y} = \frac{f(x,y)}{f_X(x)}²²

Propriétés

²\int_{\R} f(y|x) dy = 1²
²f(x,y) = f(y|x) f_X(x) = f(x|y) f_Y(y)²
²f_Y(y) = \int_{\R} f(y|x) f_X(x) dx² et ²f_X(x) = \int_{\R} f(x|y) f_Y(y) dy²

"Formule de Bayes" sur les lois

²²f(x|y) = \frac{f(y|x) f_X(x)}{f_Y(y)} = \frac{f(y|x) f_X(x)}{\int_{\R} f(y|u) f_X(u) du}²²

Exemple

Soit ²D² le domaine défini par ²²D = \{0 < x < 1 \, , \, 0 < y < 1 \}²² et ²(X, Y)² un couple de densité ²²f(x,y) = \left\{ \begin{align*} &4 x (1 - y) \text{ si } (x,y) \in D\\ &0 \quad \text{sinon} \end{align*} \right.²² Loi conditionnelle de ²X² sachant ²Y = y \in ]0,1[² ?

Solution

²²f(x|y) = \frac{f(x,y)}{f_Y(y)} = \frac{x (1 - y)}{\int_{0}^{1} x (1-y) dx} = 2 x²²

²²F(x,y) = \int_{0}^{x} \int_{0}^{y} f(x,y) dx dy = x^2 y (2 - y)²²

Espérance conditionnelle

Conditionnellement à un évènement

Cas discret

²X² et ²Y² VAr. discrètes. ²²\E[X|Y = y] = \sum_{x \in X(\Omega)} x \P(X = x|Y = y)²² (espérance de ²X² par rapport à la mesure de probabilité conditionnelle ²\P(.|Y=y)²)

Cas continu

²X² et ²Y² VAr. à densité. ²²\E[X|Y = y] = \int_{x \in \R} x f(x| y) dx²²

Conditionnellement à une VA

Définition 1 :
On note ²\psi² la fonction qui à ²y² associe ²\E[X|Y=y]². Alors ²\psi(Y)² est une VA appelée espérance de ²X² conditionnée par ²Y²

Définition 2 :
Soit ²\cS² une sous-tribu de ²\cT² dans ²(\Omega,\cT,\P)². Soit ²X² une VAr. intégrable. Alors il existe une VAr. ²Z² ²\cS²-mesurable vérifiant ²²\forall U \text{ VA. } \cS\text{-mesurable} \, , \quad \E[XU] = \E[ZU]²² On note ²Z = \E[X|\cS]²

²\Rightarrow² On retrouve la définition 1 en posant ²\E[X|Y] = \E[X|\sigma(Y)]²
Voir p.ex. la page Wikipedia comme point de départ

Théorème "de l'espérance totale"

²²\E[X] = \E[\E[X|Y]]²²

Application utile :
Calcul de ²\E\left[\sum_{n=1}^{N} X_n\right]² avec ²X_n² VA. indépendantes de même loi, et ²N² VA. discrète ²²\begin{align*} \E\left[\sum_{n=1}^{N} X_n\right] &= \E\left[ \E\left[\sum_{n=1}^{N} X_n \Bigg| N \right] \right]\\ &= \sum_{n \in N(\Omega)} \E\left[\sum_{n=1}^{N} X_n \Bigg| N = n \right] \P(N = n)\\ &= \sum_{n \in N(\Omega)} \E\left[\sum_{k=1}^{n} X_k \right] \P(N = n)\\ &= \sum_{n \in N(\Omega)} n \E[X_1] \P(N = n)\\ &= \E[X_1] \E[N] \end{align*}²²

Simulation de variables aléatoires

On a souvent besoin de simuler un ensemble de résultats selon une loi fixée.

Exemples :

Méthodes de Monte-Carlo
Cryptographie
Comportement adverse dans un jeu vidéo
...

Hypothèse

On suppose disposer d'un générateur de nombres aléatoires uniformément répartis dans £[0,1]£. On le note U.

Cas discret

Exemple 1 : loi de Bernouilli

Un évènement £A£ se réalise avec la probabilité £p£. On cherche à simuler une VA qui prenne la valeur 1 avec probabilité £p£, et 0 sinon.

²U := ALEA²
²X := 0²
if ²U < p²
²X := 1²
return ²X²

Remarque : ²X = \1_{U < p}²

Exemple 2 : généralisation

Simuler une réalisation de £X£ avec £\P(X = k) = \pi_k£, £\sum_{k=1}^{K} \pi_k = 1£.

²U := ALEA²
for ²k² in ²1:K-1²
si ²U < \sum_{i=1}^{k} \pi_i²
return ²k²
return ²K²

Remarque : ²X = \sum_{k=1}^{K} k \1_{p_{k-1} \leq U < p_k}²

La méthode revient à découper ²[0,1]² en ²K² morceaux de longueurs respectives ²p_k² :

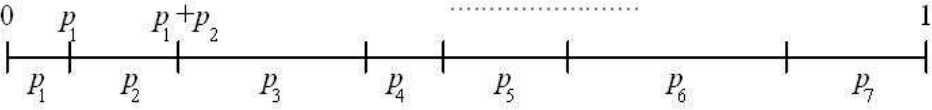
Loi de Poisson

²X \sim \cP(\lambda) \Rightarrow X(\Omega) = \N²
²p_k = \P(X = k) = e^{-\lambda} \frac{\lambda^k}{k!}²
²P_n = \sum_{k=1}^{n} p_k²

²²\left\{ \begin{align*} p_{k+1} &= \frac{\lambda}{k+1} p_k\\ P_{n+1} &= P_n + p_{k+1} \end{align*} \right.²²

Donc on peut choisir ²X = \sum_{n \geq 0} n \1_{P_{n-1} \leq U < P_n}²

Autre méthode

"Une autre méthode de simulation de VA de Poisson est issue d'une des propriétés des processus de Poisson. Si des évènements surviennent à des dates séparées par des durées exponentielles de paramètre ²\lambda², le nombre d'évènements survenant en une unité de temps suit une loi de Poisson de même paramètre."

On peut donc simuler ²²X = \sum_{n \geq 0} n \1_{Z_n \leq 1 < Z_{n+1}}²² avec ²Z_n = \sum_{k=1}^{n} Y_k² où ²Y_k \sim \cE(\lambda)²

Méthode par inversion de la f. de r.

Soit ²F² la f. de r. de ²X² et ²U \sim \cU([0,1])²

Cas inversible

²F^{-1}(U)² a même loi que ²X²

Algorithme : ²x \leftarrow F^{-1}(ALEA)²

Cas général

²F^{-} = \inf \{ t \in \R \, / \, F(t) \geq x \}²

Algorithme : ²x \leftarrow F^{-}(ALEA)²

Remarque : le cas général correspond au principe appliqué aux slides précédents

Exemples

²X \sim \cE(\lambda)²

²F(x) = 1 - e^{-\lambda x} \Rightarrow \frac{-1}{\lambda} \ln (1 - F(x)) = x²

Donc on simule ²X \leftarrow -\frac{\ln U}{\lambda}² car ²U² et ²1-U² ont même loi.

²X \sim \cN(\mu,\sigma)²

Il suffit de simuler ²\cN(0,1)² puis d'appliquer la transformation ²X \leftarrow \sigma X + \mu²

Cependant, ²F^{-1}² n'a pas d'expression simple...

(Il faudra donc procéder autrement)

Algorithme de rejet

Idée générale : simuler une VA simple, et "rejeter" les réalisations non conformes avec la VA plus élaborée que l'on souhaite obtenir.

Illustration : loi uniforme sur le domaine £B£

Probabilités conditionnelles et rejet

Cas général : simulation de £X | C£ où £C£ est une condition particulière.

Algorithme :

répéter l'expérience
X := résultat
jusqu'à ce que £C£ soit réalisée

Exemple : simulation d'un dé à 3 faces

répéter
U := dé(6)
jusqu'à (U < 4)
X := U

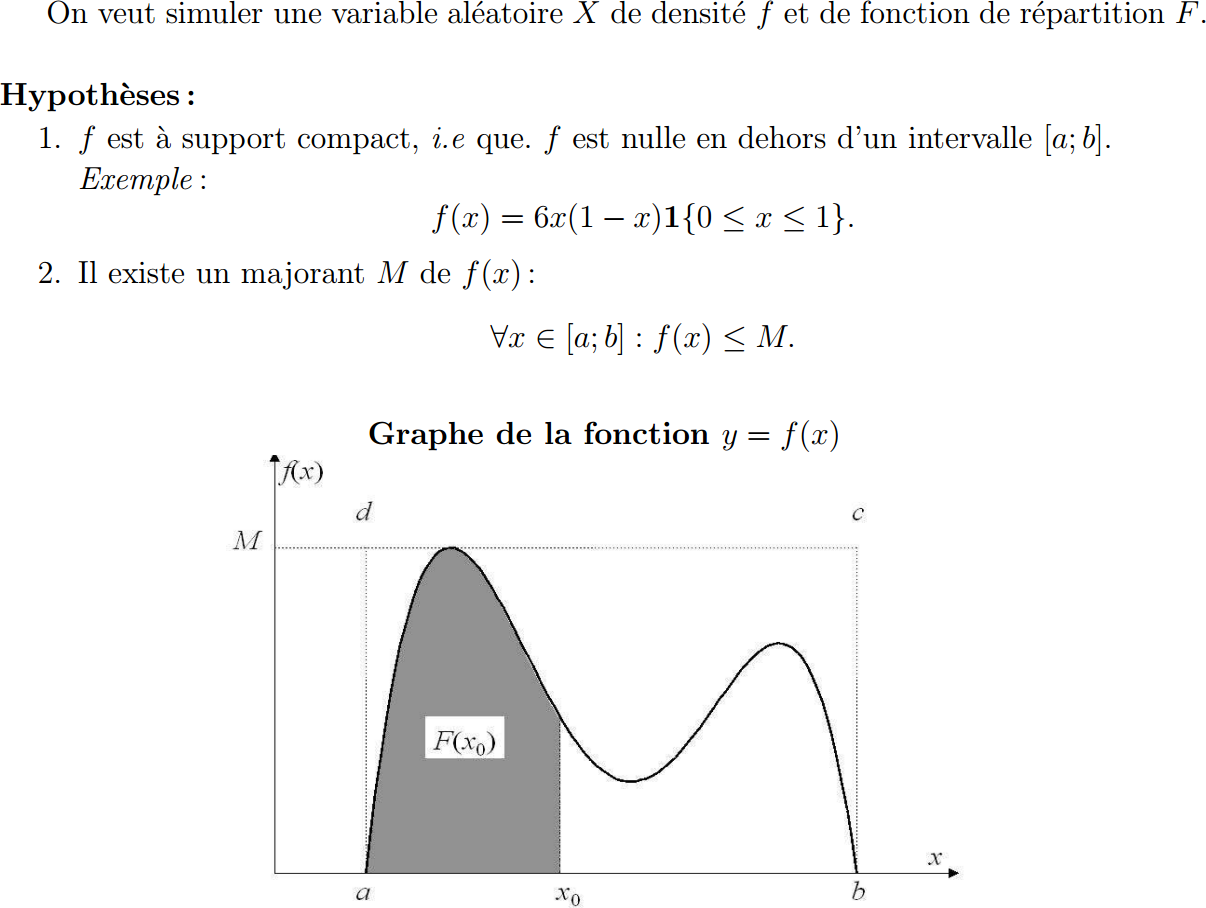
Surface du rectangle = ²M (b-a)²
Surface sous la courbe = 1
Surface de la zone grisée : ²F(x_0)²

Méthode (boucle)

On tire un point uniformément sur le rectangle : ²²X := a + (b-a) ALEA \text{ puis } Y := M ALEA²²
On garde ²X² ssi. ²Y \leq f(X)²

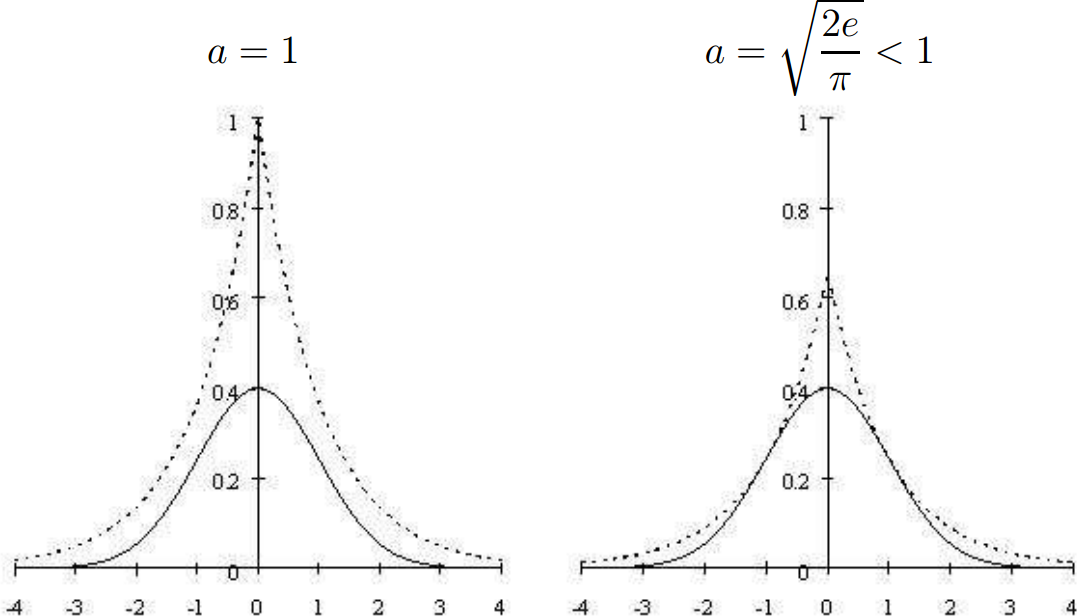
Extension aux supports non compacts

On suppose ²f² à support non borné. Si ²f \leq a \, g² avec ²g² facile à simuler, alors on peut appliquer l'algorithme suivant (²F², ²G² f. de r.)

On tire un point ²(X, Y)² distribué selon ²G² en abscisse, et ²\cU([0,a\, g])² en ordonnée.
Si ²f(X) \leq Y² on garde le tirage, ...etc

Méthode de Box-Müller

On veut simuler ²X,Y \sim \cN(0,1)² indépendantes.

Densité ²f_{X,Y}(x,y) = \frac{1}{2\pi} \exp \left( - \frac{x^2 + y^2}{2} \right)²

Passage en coordonnées polaires ²x = \rho \cos \theta², ²y = \rho \sin \theta² : ²²f_{X,Y}(x,y) dx dy = \frac{1}{2\pi} e^{-\frac{\rho^2}{2}} \rho d\rho d\theta = f_{R,\Theta}(\rho,\theta) \rho d\rho d\theta²²

Calcul des fonctions de répartition : ²²\begin{align*} F_{R^2}(\rho^2) &= 1 - e^{-\frac{\rho^2}{2}}\\ F_{\Theta}(\theta) &= \frac{\theta}{2 \pi} \end{align*}²² On reconnaît les lois exponentielle et uniforme.

(Note : source web)