Prépublication d'Orsay numéro 56 (24/9/1998)
THEORIE D'IWASAWA ET LOI EXPLICITE DE RECIPROCITE
(UN REMAKE D'UN ARTICLE DE P.COLMEZ).
PERRIN-RIOU, Bernadette - Arithmétique et Géométrie
Algébrique, Université Paris-Sud, Bât. 425, 91405 Orsay
cedex
Mots Clés : Représentations P-adiques; Théorie
d'Iwasawa; Exponentielle; Réciprocité.
Classification MSC : 11E95; 11G40; 11R23; 11R42.
Résumé :
-
Soit V une représentation p-adique cristalline du groupe
de Galois absolu de
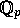 . L'auteur a élaboré la théorie d'Iwasawa d'une telle
représentation dans un article à Invent. Math (1994) et
conjecturé une loi de réciprocité. Celle-ci a
été démontrée par P. Colmez (Annals of Math).
Nous avons dans ce texte réécrit à la fois la construction
initiale en la simplifiant et la démonstration de P. Colmez dans un
langage un peu différent. Ce point de vue nous permettra dans un article
ultérieur d'étudier les normes universelles dans les classes
de cohomologie géométriques associées à la
représentation par Bloch et Kato.
. L'auteur a élaboré la théorie d'Iwasawa d'une telle
représentation dans un article à Invent. Math (1994) et
conjecturé une loi de réciprocité. Celle-ci a
été démontrée par P. Colmez (Annals of Math).
Nous avons dans ce texte réécrit à la fois la construction
initiale en la simplifiant et la démonstration de P. Colmez dans un
langage un peu différent. Ce point de vue nous permettra dans un article
ultérieur d'étudier les normes universelles dans les classes
de cohomologie géométriques associées à la
représentation par Bloch et Kato.
Abstract :
-
Let V be a crystalline p-adic representation of the absolute
Galois group of
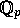 . The author has built the Iwasawa theory of such a representation in Invent.
Math (1994) and conjectured a reciprocity law which has been proved by P.
Colmez. In this text, we write the initial construction with simplification
and the proof of P. Colmez in a different langage. This point of view will
allow us to study the universal norms in the geometric cohomology classes
associated to V by Bloch and Kato in a forthcoming article.
. The author has built the Iwasawa theory of such a representation in Invent.
Math (1994) and conjectured a reciprocity law which has been proved by P.
Colmez. In this text, we write the initial construction with simplification
and the proof of P. Colmez in a different langage. This point of view will
allow us to study the universal norms in the geometric cohomology classes
associated to V by Bloch and Kato in a forthcoming article.
Article :
Documenta Mathematica 4 (1999), 215-269
Contact :
bpr@geo.math.u-psud.fr