d+1 fonctions continues à valeurs complexes, on considère
le polynôme fibré :
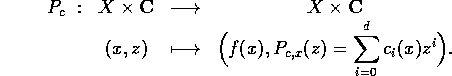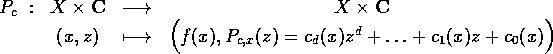
L'étude dynamique de cette application est étroitement reliée à celle des polynômes d'une variable complexe (qui correspondent au cas où X est un point). Dans notre cadre, le premier pas consiste à étendre les notions usuelles d'ensemble de Julia rempli et de fonction de Green associée. Nous définissons également à l'aide de pseudoorbites des ouverts qui jouent le rôle des bassins des orbites périodiques attractives.
Nous focalisons ensuite notre étude sur le cas quadratique (d=2). Nous caractérisons de plusieurs manières équivalentes les paramètres qui correspondent dans le cadre habituel à la cardioïde principale de l'ensemble de Mandelbrot.
Les quatre autres chapitres de la thèse commencent une description combinatoire, à la ``Douady-Hubbard'', des ensembles de Julia fibrés et de l'espace des paramètres.
Nous construisons, pour les polynômes fibrés dont la combinatoire s'apparente à celle des polynômes du membre réel de l'ensemble de Mandelbrot, l'espace abstrait des configurations. Celui-ci est un compact connexe et jouit d'une propriété universelle en relation avec les polynômes fibrés considérés.
Le résultat principal de cette thèse peut être vu comme une généralisation du théorème de Thurston sur la caractérisation des revêtements ramifiés du plan critiquement finis. Nous prouvons qu'une configuration abstraite qui est faiblement récurrente (d'un point de vue combinatoire) est réalisable de manière unique. La démonstration consiste dans un premier temps, à réaliser certaines configurations non-récurrentes. Ensuite, nous obtenons le polynôme fibré recherché comme limite uniforme de polynômes non-récurrents, le passage d'une approximation à une autre se faisant par un procédé de chirurgie.
.