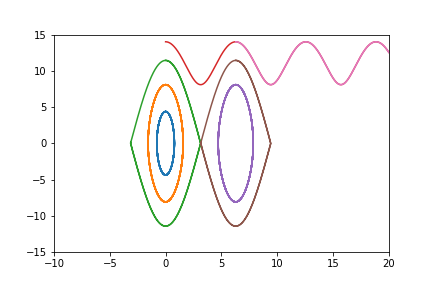
Exercice 1.- Pendule simple sans frottements.¶
Une masse ponctuelle $m$ est accrochée au bout d'une tige rigide de longueur $l$ (et de masse considérée nulle). On place l'origine du repère au point d'attache de la tige et on note $\theta$ l'angle orienté entre l'axe vertical et la tige. On rappelle que le mouvement du pendule est décrit par l'équation différentielle $$ \tag{E} \theta''(t) + \frac{g}{l} \sin ( \theta(t) ) = 0 \: , $$ où $g = 9.80665$ est l'accélération de la pesanteur à la surface de la Terre. On prendra $l = 0.3$ ($30$ cm). On pose $\omega_0 = \sqrt{\frac{g}{l}}$.
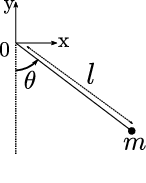
En posant $v = \theta^\prime$, mettre l'équation différentielle $(E)$ sous la forme d'un système différentiel $(E_1)$ d'ordre $1$ portant sur $\displaystyle \left( \begin{array}{c} \theta \\ v \end{array} \right)$.
Modifier la fonction
pointMilieu1Dimplémentée dans le précédent TP en une fonctionpointMilieuMultiDafin de traiter le cas multidimensionnel $y \in \mathbb{R}^d$, $d \in \mathbb{N}^\ast$. La fonctionpointMilieuMultiDaura les mêmes arguments et la même structure que dans le cas $1D$, sauf quey0sera maintant unnumpy array. On retrouvera ainsi la dimension $d$ pard = y0.size. La fonction renverra une liste[tps, sol]oùtpsest toujours le vecteur $[t_0, \ldots, t_N]$ etsolest unnumpy ndarrayde taille(tps.size, y0.size).
En faisant attention, il suffit de modifier légèrement deux lignes ...