Dulac: resummation-theoretic proof.
Dulac: constructive proof.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Avant-propos.
(janvier 1991).
Le présent ouvrage, qui dans sa conception originelle devait se
limiter à la preuve de la "conjecture de Dulac'' (finitude des
cycles-limite pour un champ de vecteurs polynomial sur 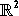 ), a changé de nature en cours de
rédaction
et s'est mué en quelque chose de nettement plus ample. Sous sa
forme actuelle, le livre illustre plusieurs techniques-clef de
resommation. Surtout, il introduit deux nouvelles classes de fonctions:
les fonctions analysables et les fonctions cohésives
, qui semblent promises à de nombreuses applications. Quant à la
preuve proprement dite de la conjecture de Dulac, elle est délibérément
traitée comme un exercice de resommation et n'occupe plus
que deux chapitres sur un total de dix. Les deux chapitres en question
sont particulièrement longs, mais leur longueur tient pour une
part aux à-cotés et aux compléments qu'ils comportent.
), a changé de nature en cours de
rédaction
et s'est mué en quelque chose de nettement plus ample. Sous sa
forme actuelle, le livre illustre plusieurs techniques-clef de
resommation. Surtout, il introduit deux nouvelles classes de fonctions:
les fonctions analysables et les fonctions cohésives
, qui semblent promises à de nombreuses applications. Quant à la
preuve proprement dite de la conjecture de Dulac, elle est délibérément
traitée comme un exercice de resommation et n'occupe plus
que deux chapitres sur un total de dix. Les deux chapitres en question
sont particulièrement longs, mais leur longueur tient pour une
part aux à-cotés et aux compléments qu'ils comportent.
Les fonctions analysables (réelles) sont grosso modo
la cloture naturelle de l'algèbre des germes (en 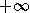 , par commodité technique) de
fonctions analytiques (réelles) relativement aux opérations
, par commodité technique) de
fonctions analytiques (réelles) relativement aux opérations 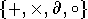 et à leurs inverses (
et à leurs inverses ( 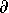 désigne la dérivation et
désigne la dérivation et  la
composition). Les fonctions analysables
la
composition). Les fonctions analysables 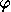 ont la distinction d' etre entièrement
formalisables, c'est-à-dire réductibles à des transséries
formelles
ont la distinction d' etre entièrement
formalisables, c'est-à-dire réductibles à des transséries
formelles 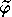 , qui se présentent comme des sommes bien ordonnées de
transmonomes , qui sont eux-memes des échafaudages irréductibles
de coefficients réels et de symboles
, qui se présentent comme des sommes bien ordonnées de
transmonomes , qui sont eux-memes des échafaudages irréductibles
de coefficients réels et de symboles 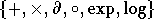 . La trigèbre des fonctions analysables
est meme, en un certain sens, la plus grande famille de germes qui
soient totalement formalisables et donc totalement "transparents''.
Toutefois, les transséries
. La trigèbre des fonctions analysables
est meme, en un certain sens, la plus grande famille de germes qui
soient totalement formalisables et donc totalement "transparents''.
Toutefois, les transséries 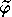 qui leur correspondent
sont génériquement divergentes, si bien que la reconstitution de
l'objet géométrique
qui leur correspondent
sont génériquement divergentes, si bien que la reconstitution de
l'objet géométrique 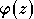 à
partir de l'objet formel
à
partir de l'objet formel 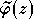 implique un délicat processus d' accéléro-sommation , qui
consiste à passer par un nombre fini de "modèles'' intermédiaires
implique un délicat processus d' accéléro-sommation , qui
consiste à passer par un nombre fini de "modèles'' intermédiaires 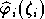 reliés les uns aux
autres par des opérateurs d'accélération , transmutés par
Borel-Laplace des changements de variable
reliés les uns aux
autres par des opérateurs d'accélération , transmutés par
Borel-Laplace des changements de variable 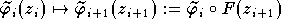 . Notons que Dubois
Reymond et surtout Hardy semblent avoir pressenti l'existence d'une
classe de fonctions analogue à celle des fonctions analysables, de
taille et de stabilité maximales, mais que l'absence d'une théorie
sommatoire adéquate les a
empechés d'aller jusqu'au bout de leur intuition.
. Notons que Dubois
Reymond et surtout Hardy semblent avoir pressenti l'existence d'une
classe de fonctions analogue à celle des fonctions analysables, de
taille et de stabilité maximales, mais que l'absence d'une théorie
sommatoire adéquate les a
empechés d'aller jusqu'au bout de leur intuition.
Selon la nature de l'accélération ("faible" ou non) reliant les
deux modèles consécutifs 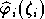 et
et 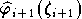 ,l'accélérée
,l'accélérée 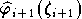 se présente comme un germe de fonction
cohésive ou analytique , possédant toujours un
développement unique (généralement ramifié) au-dessus de
se présente comme un germe de fonction
cohésive ou analytique , possédant toujours un
développement unique (généralement ramifié) au-dessus de 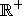 La classe des fonctions
cohésives englobe les plus "régulières" des classes
quasianalytiques de Carleman, mais elle possède toutes les propriétés
de régularité qui faisaient défaut à ces dernières. Rétrospectivement,
ces deux notions d'analysabilté et cohésivité
m'apparaissent comme les idées-force du livre. Leur imbrication est
étroite et n'a rien de fortuit. C'est précisément la cohésivité des
accélérées qui permet de les prolonger d'une facon unique. Mais il y a
plus : non seulement
les accélérées "faibles" sont cohésives mais, comme on le verra à la
fin du livre, toute fonction cohésive est une accélérée faible.
La classe des fonctions
cohésives englobe les plus "régulières" des classes
quasianalytiques de Carleman, mais elle possède toutes les propriétés
de régularité qui faisaient défaut à ces dernières. Rétrospectivement,
ces deux notions d'analysabilté et cohésivité
m'apparaissent comme les idées-force du livre. Leur imbrication est
étroite et n'a rien de fortuit. C'est précisément la cohésivité des
accélérées qui permet de les prolonger d'une facon unique. Mais il y a
plus : non seulement
les accélérées "faibles" sont cohésives mais, comme on le verra à la
fin du livre, toute fonction cohésive est une accélérée faible.
Venons-en maintenant à la conjecture de Dulac. Cette conjecture,
que Dulac avait d'ailleurs présentée comme un théorème, mais en
l'étayant par des arguments qui n'avaient que l'apparence d'une
démonstration, affirme qu'un champ de vecteurs X sur 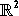 à coefficients polynomiaux
possède au plus un nombre fini de cycles-limite, i.e. de trajectoires
analytiques closes et isolées. Il suffit de montrer que ces
cycles-limite ne peuvent pas s'accumuler et, comme l'accumulation ne
pourrait se produire que sur un polycycle
à coefficients polynomiaux
possède au plus un nombre fini de cycles-limite, i.e. de trajectoires
analytiques closes et isolées. Il suffit de montrer que ces
cycles-limite ne peuvent pas s'accumuler et, comme l'accumulation ne
pourrait se produire que sur un polycycle 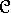 (éventuellement réduit à un point ou
à un cycle), tout revient à étudier l'application
(éventuellement réduit à un point ou
à un cycle), tout revient à étudier l'application 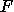 , dite de (premier) retour, associée au
polycycle
, dite de (premier) retour, associée au
polycycle 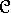 , et à
montrer la finitude de ses points fixes isolés, puisque ceux-ci
correspondent aux cycles-limite. Il n'est d'ailleurs pas nécessaire de
supposer le champ X polynomial : il suffit de le supposer
défini et analytique au voisinage de
, et à
montrer la finitude de ses points fixes isolés, puisque ceux-ci
correspondent aux cycles-limite. Il n'est d'ailleurs pas nécessaire de
supposer le champ X polynomial : il suffit de le supposer
défini et analytique au voisinage de 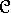 .
.
La méthode suivie consiste à décomposer l'application de retour 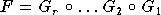 en un produit de facteurs
en un produit de facteurs 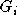 , qui sont les applications de passage
associées à chacun des sommets du polycycle, puis à envisager la
contrepartie formelle
, qui sont les applications de passage
associées à chacun des sommets du polycycle, puis à envisager la
contrepartie formelle 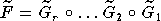 de ces applications.
Selon les sommets, les facteurs
de ces applications.
Selon les sommets, les facteurs 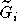 se présentent soit comme
des séries formelles, soit comme des transsériesw assez élémentaires.
La composée
se présentent soit comme
des séries formelles, soit comme des transsériesw assez élémentaires.
La composée 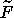 , au
contraire, revet la forme d'une transsérie générale, avec des
empilements d'exponentielles-logarithmes de complexité potentiellement
maximale. Toutefois, cette transsérie
, au
contraire, revet la forme d'une transsérie générale, avec des
empilements d'exponentielles-logarithmes de complexité potentiellement
maximale. Toutefois, cette transsérie 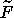 est toujours accéléro-sommable .
Sa somme
est toujours accéléro-sommable .
Sa somme 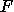 est donc une fonction
analysable qui, si elle diffère de l'application identique, ne peut
posséder que des points fixes isolés.
est donc une fonction
analysable qui, si elle diffère de l'application identique, ne peut
posséder que des points fixes isolés.
La démonstration est répartie sur deux chapitres. Le chapitre 3,
qui est une étude locale, décrit minutieusement les
facteurs 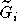 et
et
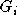 associés aux différents
sommets. Le chapitre 4, qui est une étude globale, intègre toute cette
information pour aboutir à une description exhaustive de l'application
de
retour
associés aux différents
sommets. Le chapitre 4, qui est une étude globale, intègre toute cette
information pour aboutir à une description exhaustive de l'application
de
retour 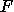 et du passage de
et du passage de 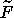 à
à 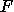 . Ainsi qu'on l'a signalé, ces deux
chapitres se veulent une défense et illustration de la théorie de
la resommation . Ils mettent en oeuvre une bonne dizaine de
méthodes, d'outils et de concepts nouveaux : résurgence, dérivées
étrangères, accélérations, médianisation, compensateurs, émanation,
transmonomes et transséries,
analysabilité, cohésivité, singularités cohésives,
quartage, douceur etc ..., qui toutes trouvent à s'appliquer
à ce problème particulier, mais dont la portée est
beaucoup plus générale. Ajoutons que la présente étude a été écrite
sans aucun souci du 16ème
problème de Hilbert, meme si celui-ci parait etre l'objectif, pour
ne pas dire l'obsession, de la plupart des mathématiciens qui
s'intéressent
au problème de Dulac.
. Ainsi qu'on l'a signalé, ces deux
chapitres se veulent une défense et illustration de la théorie de
la resommation . Ils mettent en oeuvre une bonne dizaine de
méthodes, d'outils et de concepts nouveaux : résurgence, dérivées
étrangères, accélérations, médianisation, compensateurs, émanation,
transmonomes et transséries,
analysabilité, cohésivité, singularités cohésives,
quartage, douceur etc ..., qui toutes trouvent à s'appliquer
à ce problème particulier, mais dont la portée est
beaucoup plus générale. Ajoutons que la présente étude a été écrite
sans aucun souci du 16ème
problème de Hilbert, meme si celui-ci parait etre l'objectif, pour
ne pas dire l'obsession, de la plupart des mathématiciens qui
s'intéressent
au problème de Dulac.
Tachons maintenant de répondre à deux question qu'on peut
légitimement se poser concernant la preuve de la conjecture de
Dulac présentée dans ce livre. Cette preuve est-elle la
seule possible ? Et quelle est sa longueur véritable ? La longueur
d'abord. Si l'on admet (c'est-à-dire si l'on considère comme extérieurs à la preuve )
les éléments
de la théorie des fonctions analysables et en particulier la stabilité
de ces fonctions par composition, tout se ramène à démontrer
l'analysabilité des facteurs 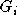 pris isolément, ce qui ne demande pas
plus d'une dizaine de pages. Si on contraire, comme nous l'avons fait
dans ce livre, on
tient à construire la notion de fonction analysable à partir
de zéro et à établir les principaux résultats de stabilité, on a
évidemment une démonstration
beaucoup plus longue (peut-etre cent pages incompressibles) mais riche
en retombées puisqu'on édifie, à son propos, une
théorie susceptible de très nombreuses applications (notamment
en théorie des équations différentielles ou fonctionnelles).
Voyons maintenant la question de l'unicité de la preuve. Les fonctions
analysables vraiment générales ne peuvent pas s'étudier
autrement que par les méthodes de ce livre. Mais l'application de
retour
pris isolément, ce qui ne demande pas
plus d'une dizaine de pages. Si on contraire, comme nous l'avons fait
dans ce livre, on
tient à construire la notion de fonction analysable à partir
de zéro et à établir les principaux résultats de stabilité, on a
évidemment une démonstration
beaucoup plus longue (peut-etre cent pages incompressibles) mais riche
en retombées puisqu'on édifie, à son propos, une
théorie susceptible de très nombreuses applications (notamment
en théorie des équations différentielles ou fonctionnelles).
Voyons maintenant la question de l'unicité de la preuve. Les fonctions
analysables vraiment générales ne peuvent pas s'étudier
autrement que par les méthodes de ce livre. Mais l'application de
retour 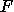 est une fonction
analysable très particulière, puisqu'elles se décompose en facteurs
est une fonction
analysable très particulière, puisqu'elles se décompose en facteurs 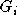 eux-memes très élémentaires, car ne
possédant chacun qu'un seul "temps critique'' et par suite sommables
par Borel-Laplace, sans recours à l'accélération.
On peut dire sans exagérer que
eux-memes très élémentaires, car ne
possédant chacun qu'un seul "temps critique'' et par suite sommables
par Borel-Laplace, sans recours à l'accélération.
On peut dire sans exagérer que 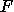 est aux "vraies'' fonctions
analysables ce que les superpositions fines
est aux "vraies'' fonctions
analysables ce que les superpositions fines 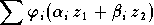 sont aux "vraies" fonctions
analytiques de deux variables. Ce caractère très spécial et
passablement élémentaire de
sont aux "vraies" fonctions
analytiques de deux variables. Ce caractère très spécial et
passablement élémentaire de 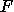 fait qu'il existe d'autres moyens d'en
aborder l'étude, notamment la méthode, géométique et non-constructive,
de Yu. S. Ilyashenko à paraitre dans [Il.2] et
basée sur une extension du principe de Lindel
fait qu'il existe d'autres moyens d'en
aborder l'étude, notamment la méthode, géométique et non-constructive,
de Yu. S. Ilyashenko à paraitre dans [Il.2] et
basée sur une extension du principe de Lindel 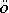 f. Il y a aussi les méthodes esquissées au §4.6 de
ce livre et basées sur des propriétés
d'indépendance (ce sont les "lemmes d'immiscibilité",
dont l'unreste encore à prouver --- mais ceux qui sont acquis suffisent
déjà simplifier grandement la preuve de la non-oscillation
de
f. Il y a aussi les méthodes esquissées au §4.6 de
ce livre et basées sur des propriétés
d'indépendance (ce sont les "lemmes d'immiscibilité",
dont l'unreste encore à prouver --- mais ceux qui sont acquis suffisent
déjà simplifier grandement la preuve de la non-oscillation
de 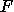 ). Il y a donc plusieurs
manières, authentiquement
différentes, de prouver la conjecture de Dulac ou, si l'on préfère,
la non-oscillation de
). Il y a donc plusieurs
manières, authentiquement
différentes, de prouver la conjecture de Dulac ou, si l'on préfère,
la non-oscillation de 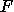 . Il me semble
toutefois que la méthode exposée dans ce livre soit la seule qui
aille au fond de la question, en
formalisant totalement l'objet géométrique
. Il me semble
toutefois que la méthode exposée dans ce livre soit la seule qui
aille au fond de la question, en
formalisant totalement l'objet géométrique 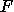 . Plus pécisément, je suis
convaincu de trois choses:
. Plus pécisément, je suis
convaincu de trois choses:
1) Le seul objet formel à coefficients réels
qu'on puisse sensément associer à 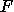 et qui en recèle toute l'information,
est
la transsérie médiane
et qui en recèle toute l'information,
est
la transsérie médiane 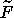 construite dans ce livre.
construite dans ce livre.
2) La seule méthode explicite et constructive permettant de
reconstituer 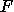 à partir de
à partir de 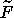 , est la méthode d'accéléro-sommation
médiane, exposée dans ce livre.
, est la méthode d'accéléro-sommation
médiane, exposée dans ce livre.
3) Seule la formalisation totale de 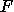 , c'est-à-dire sa réduction à l'objet
formel
, c'est-à-dire sa réduction à l'objet
formel 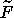 ,
peut offrir une compréhension complète de
,
peut offrir une compréhension complète de 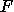 et de tout ce qu'on peut fabriquer à
partir de
et de tout ce qu'on peut fabriquer à
partir de 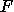 (par exemple, la
non-oscillation des dérivées succesives de
(par exemple, la
non-oscillation des dérivées succesives de 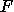 ).
).
La seconde moitié du livre (chapitres 5 à 10) comprend
des compléments qui éclairent et prolongent les méthodes mises en
oeuvre pour la résolution du problème de Dulac. Le chapitre 5 dégage
deux transformations purement formelles sous-jacentes aux
transformations fonctionnelles de Borel et de Laplace ("quartage" et
"formules cryptolinéaires"). Le chapitre 6 établit l'identité entre
les fonctions cohésives et les accélérées faibles,
puis en tire les conséquences pratiques. Les chapitres 7,8,9 montrent
que les fonctions analysables marquent en quelque sorte l'
l'ultime limite de la formalisabilité des germes ,
et qu'au-delà il n'y a plus rien qui leur ressemble. En
effet, du fait de l' asymptotique universelle des germes
lents ou rapides et du théorème d'indiscernabilité
, il n'existe plus, au-delà de l'échelle des exponentielles et des
logarithmes itérés, de fonctions-repère authentiquement canonique et
susceptibles de servir de "base" à une tentative
de formalisation des germes. Toutefois, ainsi qu'il arrive souvent en
mathématiques, ce résultat "négatif" possède
une contrepartie "positive" et fort inattendue, à savoir le caractère
essentiellement "discret" et "fractal" de l' échelle naturelle
de croissance . Tout ceci débouche sur une notion très
naturelle d'itération transfinie et sur le "Grand
Cantor" , obtenu par élimination des "zones de croissances"
qui regroupes tous les "germes indiscernables".
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Update: well-behaved averages.
xxx
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Update: J. van der Hoeven's and V. Bagayoko's work on hyperseries.
xxx
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
The non-accumulation theorem thirty years on.
xxx
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
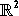 ), a changé de nature en cours de
rédaction
et s'est mué en quelque chose de nettement plus ample. Sous sa
forme actuelle, le livre illustre plusieurs techniques-clef de
resommation. Surtout, il introduit deux nouvelles classes de fonctions:
les fonctions analysables et les fonctions cohésives
, qui semblent promises à de nombreuses applications. Quant à la
preuve proprement dite de la conjecture de Dulac, elle est délibérément
traitée comme un exercice de resommation et n'occupe plus
que deux chapitres sur un total de dix. Les deux chapitres en question
sont particulièrement longs, mais leur longueur tient pour une
part aux à-cotés et aux compléments qu'ils comportent.
), a changé de nature en cours de
rédaction
et s'est mué en quelque chose de nettement plus ample. Sous sa
forme actuelle, le livre illustre plusieurs techniques-clef de
resommation. Surtout, il introduit deux nouvelles classes de fonctions:
les fonctions analysables et les fonctions cohésives
, qui semblent promises à de nombreuses applications. Quant à la
preuve proprement dite de la conjecture de Dulac, elle est délibérément
traitée comme un exercice de resommation et n'occupe plus
que deux chapitres sur un total de dix. Les deux chapitres en question
sont particulièrement longs, mais leur longueur tient pour une
part aux à-cotés et aux compléments qu'ils comportent.
 , par commodité technique) de
fonctions analytiques (réelles) relativement aux opérations
, par commodité technique) de
fonctions analytiques (réelles) relativement aux opérations 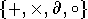 et à leurs inverses (
et à leurs inverses ( 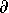 désigne la dérivation et
désigne la dérivation et  la
composition). Les fonctions analysables
la
composition). Les fonctions analysables 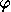 ont la distinction d' etre entièrement
formalisables, c'est-à-dire réductibles à des transséries
formelles
ont la distinction d' etre entièrement
formalisables, c'est-à-dire réductibles à des transséries
formelles 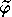 , qui se présentent comme des sommes bien ordonnées de
transmonomes , qui sont eux-memes des échafaudages irréductibles
de coefficients réels et de symboles
, qui se présentent comme des sommes bien ordonnées de
transmonomes , qui sont eux-memes des échafaudages irréductibles
de coefficients réels et de symboles 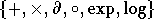 . La trigèbre des fonctions analysables
est meme, en un certain sens, la plus grande famille de germes qui
soient totalement formalisables et donc totalement "transparents''.
Toutefois, les transséries
. La trigèbre des fonctions analysables
est meme, en un certain sens, la plus grande famille de germes qui
soient totalement formalisables et donc totalement "transparents''.
Toutefois, les transséries 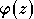 à
partir de l'objet formel
à
partir de l'objet formel 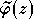 implique un délicat processus d' accéléro-sommation , qui
consiste à passer par un nombre fini de "modèles'' intermédiaires
implique un délicat processus d' accéléro-sommation , qui
consiste à passer par un nombre fini de "modèles'' intermédiaires 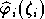 reliés les uns aux
autres par des opérateurs d'accélération , transmutés par
Borel-Laplace des changements de variable
reliés les uns aux
autres par des opérateurs d'accélération , transmutés par
Borel-Laplace des changements de variable 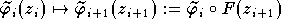 . Notons que Dubois
Reymond et surtout Hardy semblent avoir pressenti l'existence d'une
classe de fonctions analogue à celle des fonctions analysables, de
taille et de stabilité maximales, mais que l'absence d'une théorie
sommatoire adéquate les a
empechés d'aller jusqu'au bout de leur intuition.
. Notons que Dubois
Reymond et surtout Hardy semblent avoir pressenti l'existence d'une
classe de fonctions analogue à celle des fonctions analysables, de
taille et de stabilité maximales, mais que l'absence d'une théorie
sommatoire adéquate les a
empechés d'aller jusqu'au bout de leur intuition. 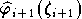 ,l'accélérée
,l'accélérée 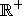 La classe des fonctions
cohésives englobe les plus "régulières" des classes
quasianalytiques de Carleman, mais elle possède toutes les propriétés
de régularité qui faisaient défaut à ces dernières. Rétrospectivement,
ces deux notions d'analysabilté et cohésivité
m'apparaissent comme les idées-force du livre. Leur imbrication est
étroite et n'a rien de fortuit. C'est précisément la cohésivité des
accélérées qui permet de les prolonger d'une facon unique. Mais il y a
plus : non seulement
les accélérées "faibles" sont cohésives mais, comme on le verra à la
fin du livre, toute fonction cohésive est une accélérée faible.
La classe des fonctions
cohésives englobe les plus "régulières" des classes
quasianalytiques de Carleman, mais elle possède toutes les propriétés
de régularité qui faisaient défaut à ces dernières. Rétrospectivement,
ces deux notions d'analysabilté et cohésivité
m'apparaissent comme les idées-force du livre. Leur imbrication est
étroite et n'a rien de fortuit. C'est précisément la cohésivité des
accélérées qui permet de les prolonger d'une facon unique. Mais il y a
plus : non seulement
les accélérées "faibles" sont cohésives mais, comme on le verra à la
fin du livre, toute fonction cohésive est une accélérée faible. 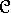 (éventuellement réduit à un point ou
à un cycle), tout revient à étudier l'application
(éventuellement réduit à un point ou
à un cycle), tout revient à étudier l'application 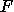 , dite de (premier) retour, associée au
polycycle
, dite de (premier) retour, associée au
polycycle 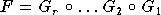 en un produit de facteurs
en un produit de facteurs 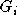 , qui sont les applications de passage
associées à chacun des sommets du polycycle, puis à envisager la
contrepartie formelle
, qui sont les applications de passage
associées à chacun des sommets du polycycle, puis à envisager la
contrepartie formelle 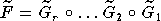 de ces applications.
Selon les sommets, les facteurs
de ces applications.
Selon les sommets, les facteurs 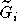 se présentent soit comme
des séries formelles, soit comme des transsériesw assez élémentaires.
La composée
se présentent soit comme
des séries formelles, soit comme des transsériesw assez élémentaires.
La composée 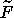 , au
contraire, revet la forme d'une transsérie générale, avec des
empilements d'exponentielles-logarithmes de complexité potentiellement
maximale. Toutefois, cette transsérie
, au
contraire, revet la forme d'une transsérie générale, avec des
empilements d'exponentielles-logarithmes de complexité potentiellement
maximale. Toutefois, cette transsérie 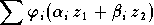 sont aux "vraies" fonctions
analytiques de deux variables. Ce caractère très spécial et
passablement élémentaire de
sont aux "vraies" fonctions
analytiques de deux variables. Ce caractère très spécial et
passablement élémentaire de 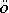 f. Il y a aussi les méthodes esquissées au §4.6 de
ce livre et basées sur des propriétés
d'indépendance (ce sont les "lemmes d'immiscibilité",
dont l'unreste encore à prouver --- mais ceux qui sont acquis suffisent
déjà simplifier grandement la preuve de la non-oscillation
de
f. Il y a aussi les méthodes esquissées au §4.6 de
ce livre et basées sur des propriétés
d'indépendance (ce sont les "lemmes d'immiscibilité",
dont l'unreste encore à prouver --- mais ceux qui sont acquis suffisent
déjà simplifier grandement la preuve de la non-oscillation
de