A visual introduction to the Giroux correspondence

This page is loosely based on a talk I gave in Max Planck Institute for mathematics in Bonn on July 2nd 2013 during the conference Interactions between low dimensional topology and mapping class groups. It is an introduction to the Giroux correspondence in dimension three.

Open books

An open book on a closed 3-manifold is a fibration over S¹ defined on the complement of a link called the binding. Each connected component B of the binding must have a tubular neighborhood B × D² where the fibration over S¹ comes from the canonical one on D² \ {0}. In particular each fiber can be compactified to a surface whose boundary is the binding. These surfaces are called pages of the open book. The following animation shows a standard neighborhood of a binding component obtained by gluing top and bottom to get a golden circle binding surrounded by blue annuli.

However, seen in a different tubular neighborhood, it could look like the following (which is the image of the preceding one under a diffeomorphism of the solid torus). Notice how the rotation around the binding is now also seen as a vertical translation.

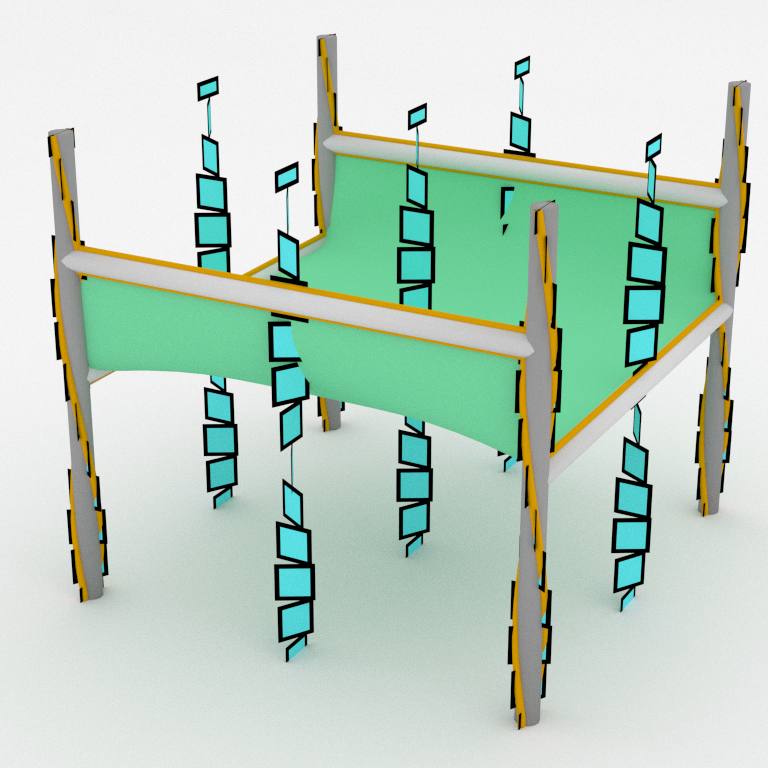
We are now ready for a global view of an open book on the 3-torus. The next animation lives inside a cube whose opposite faces are pairwise glued by translation to get 𝕋³. There are four binding components and pages have genus one.

One can generate new open books from old ones by stabilization. For any arc properly embedded in a page (green on the picture below), one can plumb an annulus such that there is an embedded disk whose interior is disjoint from the original page, whose boundary is in the annulus and such that the new binding intersects twice the new page positively.

Contact Heegaard splittings and supporting open books

The following picture represents again the 3-torus as a cube with glued faces but equiped with a plane field which is tangent to the vertical direction and rotates one full turn along each vertical circle.

By definition, a contact structure on a 3-manifold is a plane field which is locally isomorphic to the above example. The Giroux correspondence relates open books and contact structures. Before explaining that, we need a digression about Heegaard splittings.

A handlebody in a 3-manifold is a regular neighborhood of a graph. In 𝕋³, one can use the edges of our cube to get a genus 3 handlebody.

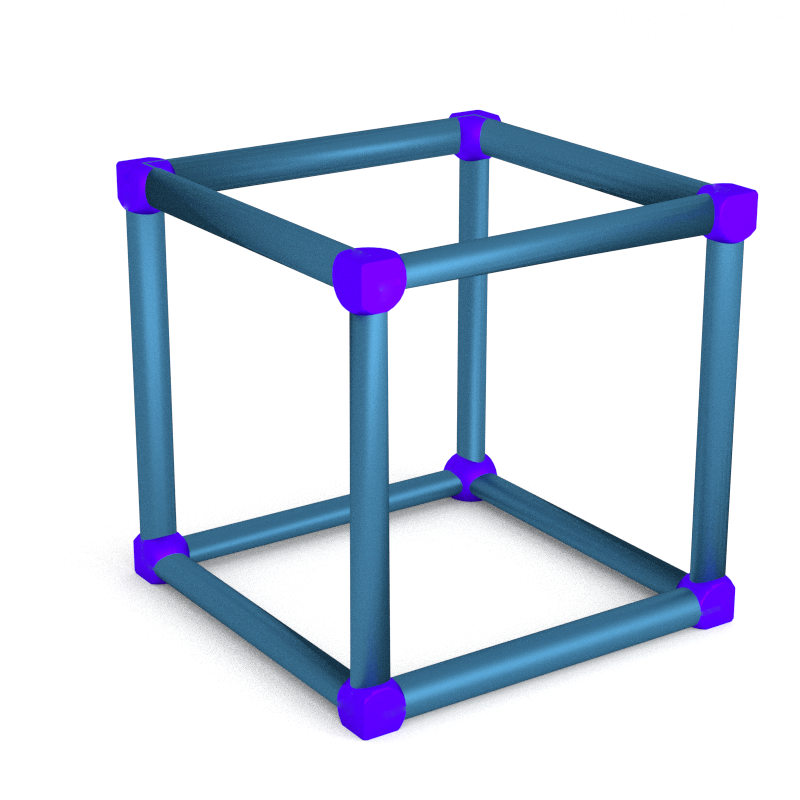
A Heegaard splitting is a decomposition into two handlebodies. So it correspond to a pair of disjoint graphs whose complement is a product of a surface and an interval. Any polyedral decomposition of a 3-manifold gives such a decomposition where one graph is the 1-skeleton and the other is the 1-skeleton of the dual decomposition.

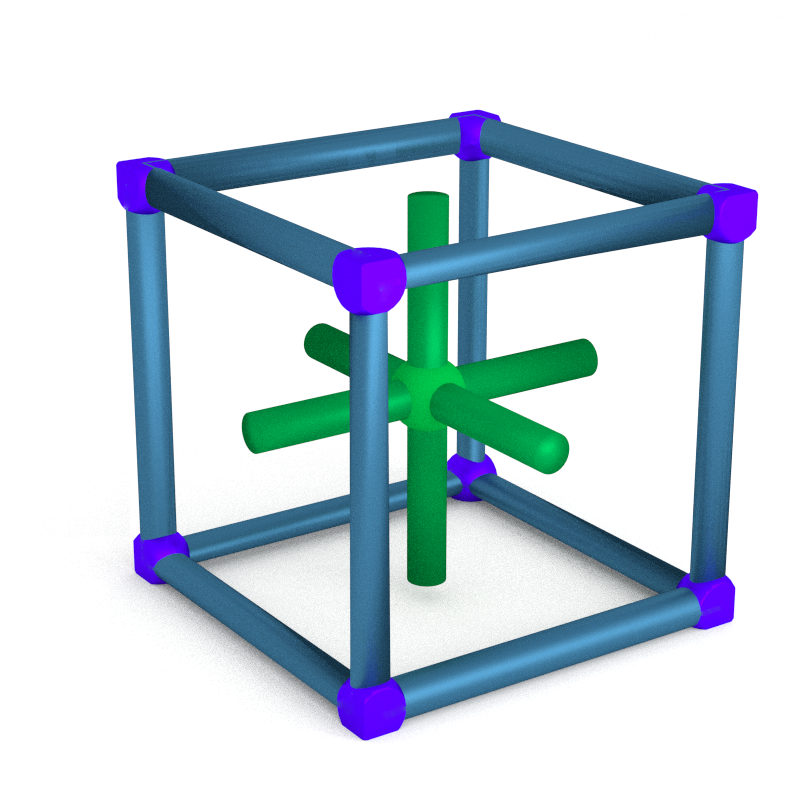
In a contact manifold, a contact handlebody is a regular neighborhood of a Legendrian graph. It is automatically cut in two halves by a properly embedded surface which is a thickening of the graph in the contact direction. In the picture below, the graph is black, the contact structure light blue, the boundary of the handlebody transparent blue, the thickening dark blue.

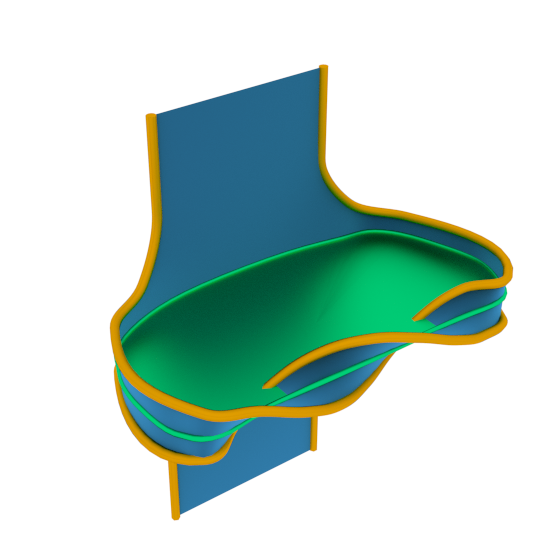
The dark blue surfaces spans a half open book whose binding is its golden intersection with the boundary of the handlebody.

Note that the binding can be connected even if the surface has higher genus.

A contact Heegaard splitting is a decomposition of a contact manifold into two contact handlebodies. It has two half open books which can be glued together to get a full open book. Giroux defined a precise relation between the open book and the contact structure which allows to go back and forth. We state it but it is not really necessary to understand the following discussion. First notice that an orientation of the circle gives a coorientation to pages. The coorientation combines with the contact orientation to orient pages and then the binding. A contact structure is then carried by an open book decomposition if there is a vector field positively transverse to the fibers and to the contact structure, positively tangent to the binding and whose flow preserves the contact structure.

In order to exhibit contact Heegaard splittings, we need a criterion to check when the complement of a contact handlebody is also a contact handlebody. A theorem essentially due to Torisu asserts that a necessary and sufficient condition is that the complement is tight and contains a set of properly embedded disks (called compression disks) which cuts it to a ball and such that each disk meets the golden binding transversely in exactly two points (this is not an algebraic count of intersections). The following picture and its green disks illustrate the easy direction: this condition is necessary.

The above criterion and the example of a contact Heegaard splitting on 𝕋³ are enough to find a contact Heegaard splitting for our contact structure on 𝕋³. We first find a Legendrian graph having a regular neighborhood isotopic to a neighborhood of edges of our cube.

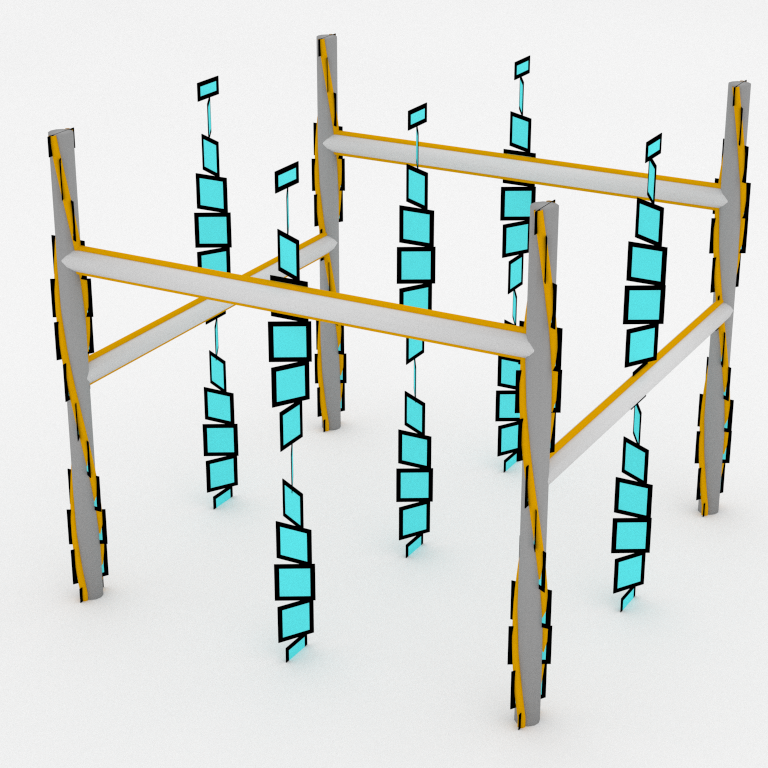
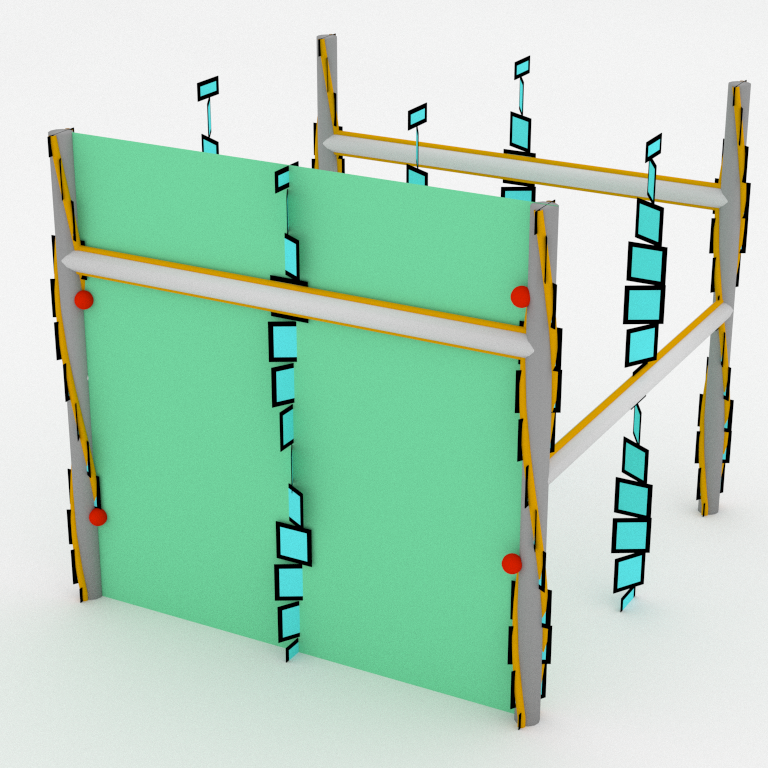
The complement of the above handlebody is tight because the whole contact manifold is a quotient of the standard ℝ³. This complement has three obvious compression disks coming from faces of the cube, isotoped to follow the graph. So we can check the intersection criterion. The disk coming from the top face intersect twice the binding.

But the disk coming from the front face has four intersection points (marked in red).

In order to get rid of excess intersections, we add a new edge to our graph through the bad disk. The disk is now split as two disk having the correct number of intersections.

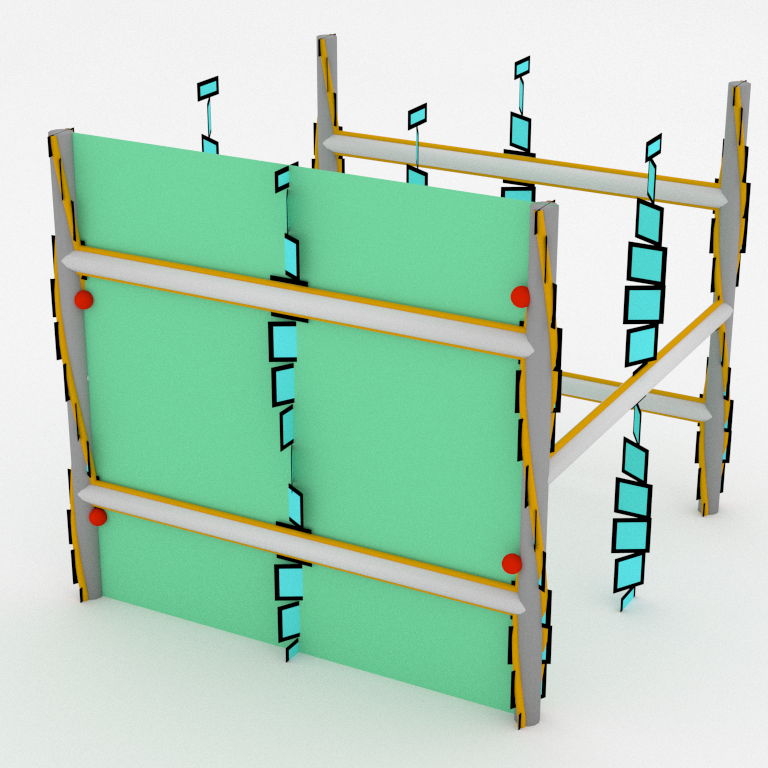
The compression disk coming from the right face can be fixed in the same way. Then we get an open book supporting the standard contact structure on 𝕋³. Giroux proved that any contact structure has a supporting open book which is unique up to isotopy and positive stabilization.