Courbe du dragon

Construction à la main:

Pour construire une courbe du dragon, il faut une bande de papier que l'on plie sur elle même. On réitère le procédé plusieurs fois dans le même sens.

Lorsque l'on déplie la bande, on laisse chacuns des plis en tant qu'angle droit dans le sens où il a été plié...

Propriété de symétrie :

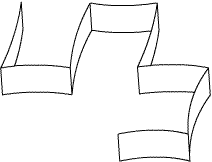
Considérons la bande de papier encore pliée (elle a été repliée sur elle-même un nombre N de fois) :

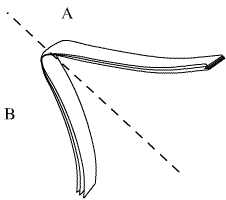
Supposons que les parties A et B de la bande sont symétriques par rapport à la droite et que A et B ont chacune, lorsqu'on les déplie la forme qu'avait la bande avait à l'étape n-1 (pliée N-1 fois sur elle même). Si l'on plie la bande sur elle même une N+1 ^ème fois et qu'on la redéplie 2 fois, l'on se retrouve dans la même situation sauf que A et B ont été pliés sur eux même et ont donc la même forme que la bande lorsqu'elle a été repliée sur elle même N fois. Donc de proche en proche on en déduit que le passage à l'étape suivant correspond à rajouter exactement le même motif au bout du précédent à un angle de 90° (toujours orienté dans le même sens) .

Construction sous Mapple :

   restart:with(geometry):point(O,[0,0]):point(C0,[1,0]):segment(Segment1,[O,C0]):
   step:=8:
   Pi/2:
   for i from 0 to step by 1 do
     tmp:=2^i:
     seq (rotation(evaln(`Segment`.(tmp+j)),evaln(`Segment`.(tmp-j+1)),Pi/2,'clockwise',evaln(`C`.i)),j=1..tmp);
     rotation(evaln(`C`.(i+1)),O,Pi/2,'clockwise',evaln(`C`.i)):
   od:
   draw({seq(`Segment`.i(color = COLOR(RGB,i/2^(step+1),0,1-i/2^(step+1))),i=1..2^(step+1))},printtext=false,axes=none);

nous permet d'obtenir les dragons par la méthode explicitée au-dessus (avec les copies et les rotations...). Il suffit d'augmenter la valeur de step pour avoir plus d'itérations.

Calcul de dragon et complexité:

Cet algorithme a une complexité d'ordre eⁿ, en effet a chaque itération 2 fois plus de segments sont créés.
Toutefois il ne faut pas oublier que la plupart du temps on cherche juste à calculer une représentation de la courbe du dragon au bout d'un certain nombre d'étapes. On travaille donc avec une résolution finie. On pourrait concevoir un algorythme qui tiendrait compte de cette donnée tout au long du calcul et non seulement à la fin pour l'affichage.
Partons avec avec une matrice d'une dimension un peu supérieure à celle voulue. Les 1 représentent des points traversés par la courbe,les 0 ,les autres. On remplirait la matrice par la rerésentation de la courbe à une certaine étape (à l'étape 0 la courbe est juste un segment). A chaque itération la transposée de la matrice serait ajoutée au bout de la courbe d'avant. Dés que l'image dépasserait la taille voulue elle serait rétrécie par 2 (la courbe n'est jamais à cheval sur 2 cases car toujours parallèle à l'un des bords. Lorsque l'on réduit la matrice on prends des groupes de 4 pixels et on regarde si l'un d'entre eux est traversé par la courbe. Si leurs somme est supérieur à 0 la case correspondants à ce groupe de pixel dans la matrice réduite est mise à un. ). La complexité en serait considérablement réduite: cet algorithme travaillerait toujours sur un nombre à peu près équivalent de pixels et aurait donc une complexité d'ordre N. On peut donc imaginer un programme qui nous calculerait en temps réel cette fractale jusqu'en la limite de ce que peut afficher l'écran.

Erratum :

tout le code source, les images, les démonstrations ont été faits par moi sans consulter de sources extérieures. Le code source n'est pas optimisé et les ébauches de démonstration peuvent certainement être clarifiée

Remerciement :