Asymptotic pairs in positive-entropy systems
Ergod. Th. & Dynam. Syst., 22, 671-686, 2002.
Abstract
We show that in a topological dynamical system (X,T) of positive
entropy there exist proper (positively) asymptotic pairs, that is, pairs (x,y)
such that x is not equal to y and 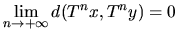 .
More precisely we consider a
T-ergodic measure
.
More precisely we consider a
T-ergodic measure 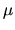 of positive entropy and prove that the
set of points that belong to a proper asymptotic pair is of measure
1. When T is invertible, the stable classes (i.e., the equivalence
classes for the asymptotic equivalence) are not stable under
T -1: for
of positive entropy and prove that the
set of points that belong to a proper asymptotic pair is of measure
1. When T is invertible, the stable classes (i.e., the equivalence
classes for the asymptotic equivalence) are not stable under
T -1: for
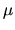 -almost every x there are uncountably many y that are asymptotic with
x and such that (x,y) is a Li-Yorke pair with respect to
T -1. We also
show that asymptotic pairs are dense in the set of topological entropy pairs.
-almost every x there are uncountably many y that are asymptotic with
x and such that (x,y) is a Li-Yorke pair with respect to
T -1. We also
show that asymptotic pairs are dense in the set of topological entropy pairs.
Paper:
[arXiv:1901.00327]
[pdf]