Compléments d’algèbre linéaire
Automne 2023
Introduction
Ce cours se place dans la lignée de la partie concernant les matrices du cours Outils mathématiques fondamentaux et Algèbre liénaire et codage que vous avez pu voir aux semestres 1 et 3. Cela sera plus approfondi avec aussi un recul théorique qui permettra de vraiment comprendre la linéarité au-delà des simples fonctions d’une variable comme vous avez pu le voir dans l’enseignement secondaire.
Ce cours introduira aussi les notions de bases, changement de bases et matrices associées que nous utiliserons dans le cours Visualisation 3D qui suit celui-ci.
0.1 Exemples d’applications de l’algèbre linéaire
De nombreux problèmes se ramènent à résoudre un système d’équations linéaires. Un certain nombre de devinettes sont de la forme suivante.
Devinette
Des lapins et des poules cohabitent dans une cour. On dénombre 128 têtes et 438 pattes.
Combien y a-t-il de poules ?
Sans méthode, il est facile de s’y perdre. Avec méthode, on appelle \(x\) le nombre de lapins et \(y\) le nombre de poules et on obtient le système suivant (les poules ayant 2 pattes et les lapins 4 pattes)
\[\left\{\begin{matrix}x+y&=128\\4x+2y&=438\end{matrix}\right.\]
En résolvant le système, on trouve \(x=91\) et \(y=37\). La réponse est donc 37 poules.
Calcul de notes d’UE
En dehors de ce genre de devinettes, on trouve des problèmes où l’algèbre linéaire et/ou l’utilisation de matrices permettent des solutions pratiques et programmables.
Voici le tableau avec les coefficients des matières par UE.
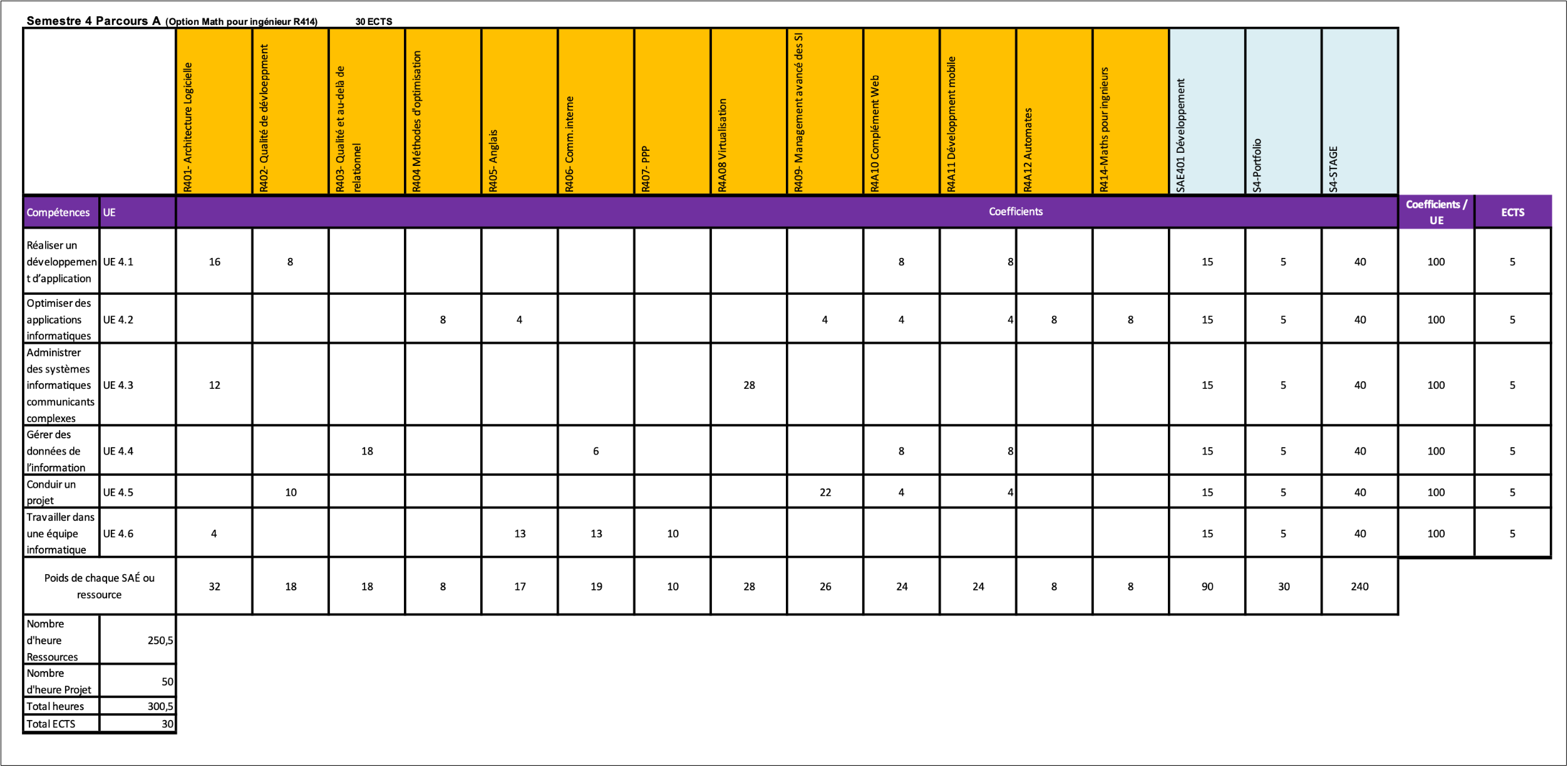
Figure 0.1: Le tableau des coefficients par UE
À partir des notes obtenues dans chaque matière, comment connaître ses notes par UE ? Il suffit de faire le produit de la matrice des coefficients avec le vecteur colonne des notes !
Lights out
Nous passerons aussi du temps à jouer à Lights out! un jeu électronique des années 1990 (auquel on peut toujours jouer en ligne (https://daattali.com/shiny/lightsout/) ) qui a pour but d’éteindre toutes les cases en appuyant sur ces cases (ce qui change aussi l’état des cases voisines). Bien que le jeu puisse semble simpliste, le résoudre n’est pas évident du tout !

Figure 0.2: Le jeu original Lights out
Nous verrons que gagner à ce jeu consiste à résoudre un système linéaire. Nous pourrons alors répondre aux questions suivantes.
- Peut-on toujours gagner à partir de n’importe quelle configuration initiale ?
- S’il y a une solution est-elle unique ?
- S’il y en a plusieurs, comment obtenir celle avec un nombre de coups minimal ?
Lors d’un TP Python, nous programmerons le jeu avec des matrices. Il y aura à la fois la programmation du jeu et un résolveur.
Perspectives et changement de point de vue
Les jeux vidéos 3D affichent en réalité des images en 2D (même les casques 3D affichent en fait deux images 2D). Comment calculer une vue 2D à partir d’une scène 3D ? Comment changer de point de vue ?
Pour répondre à ces problèmes, on fait des changements de coordonnées et des produits de matrices \(3\times 3\) ou \(4\times4\).
Un problème pratique analogue est le suivant. Une app de scan redresse un document qui apparait comme un quadrilatère quelconque sur la photo en un beau rectangle au format A4. Comment fait-elle ? Quelle est la transformation géométrique derrière ce redressement ? Nous verrons dans le cours Visualisation 3D qu’on répond à cette question en faisant de nouveau un produit de matrice.
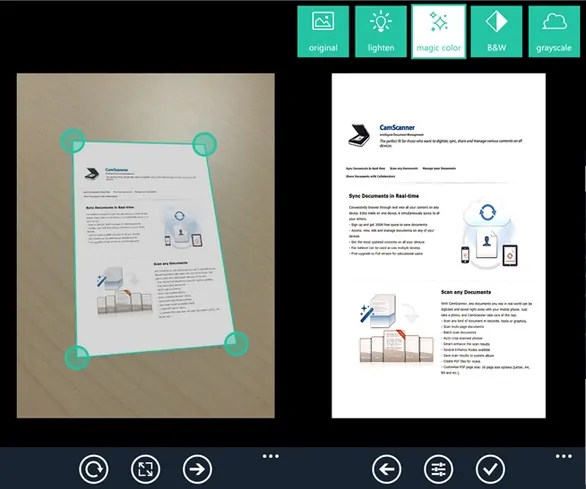
Figure 0.3: App de scan pour téléphones portables
Une image est une matrice
Nous verrons comment les images sont représentées par des matrices pour les ordinateurs. Une image en noir et blanc avec \(n\times m\) pixels sera encodée par une matrice de taille \(n\times m\) où chaque coefficient de la matrice représentera un niveau de gris. Si l’image est en couleur, il faudra une matrice pour chaque couleur primaire (Rouge, Vert et Bleu).
Une fois les images représentées par des matrices, on peut leur appliquer de l’algèbre linéaire, par exemple faire la somme de deux images.

Figure 0.4: Somme de deux images. Source : (https://hadrien-montanelli.github.io/2022-12-30.html)
Bien d’autres transformations sur les images (en fait les fichiers son et les fichiers vidéo aussi) utilisent de l’algèbre linéaire : filtres, convolution, floutage, face swapping, morphing…

Figure 0.5: Morphing de Bush vers Obama. Source : (https://studentstudyhub.com/morphing-metamorphosis-techniques-applications/)
0.2 Méthodologie
Bien qu’il s’agisse d’un cours de troisième année, il n’est pas inutile de rappeler la méthodologie pour réussir en cours de mathématiques. Les principes fondamentaux sont les suivants:
- Assiduité irréprochable en cours comme en TD,
- Reprendre le cours avant de venir en TD (relire le dernier chapitre, apprendre les définitions, connaître les énoncés des résultats démontrés)
- Être actif en TD
- Refaire les exercices de TD avant les examens et faire des exercices d’entrainement.
0.3 Alphabet grec
Souvent pour faire entre un nombre et un vecteur, nous utiliserons quelques lettres de l’alphabet grec pour les premiers et l’alphabet latin pour les seconds. Voici les principales lettres minuscules de l’alphabet grec utilisées en mathématiques.
| Lettre grecque | Nom | |
|---|---|---|
| \(\alpha\) | alpha | |
| \(\beta\) | beta | |
| \(\gamma\) | gamma | |
| \(\delta\) | delta | |
| \(\epsilon\) | epsilon | |
| \(\theta\) | thêta | |
| \(\lambda\) | lambda | |
| \(\mu\) | mu | |
| \(\pi\) | pi | |
| \(\rho\) | rho | |
| \(\sigma\) | sigma | |
| \(\tau\) | tau | |
| \(\phi\) | phi | |
| \(\psi\) | psi | |
| \(\omega\) | omega |