Convex surfaces

Introduction

This page shows examples of various key phenomena in the elementary theory of Giroux's convex surfaces (see my lecture notes). The ambiant contact manifold is always the space of cooriented lines tangent to a torus equiped with its canonical contact structure. It is drawn as a cube with opposite faces glued by translation. All pictures on this page come from the same blender file xit3.blend (it was created with blender 2.58 but certainly works with any later version or even 2.49x). See my blender page for indications on how to use this file.

Genericity

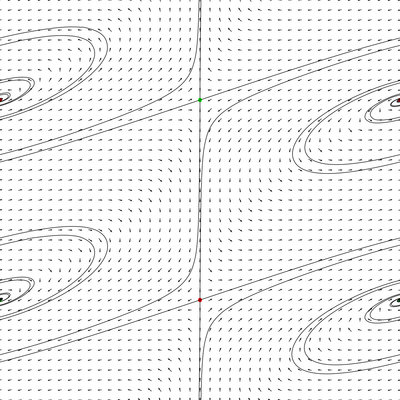
The easiest example of a surface which is not convex is a perfectly horizontal torus. It has a linear foliation whose direction depends on its height. The following example is foliated by circles.

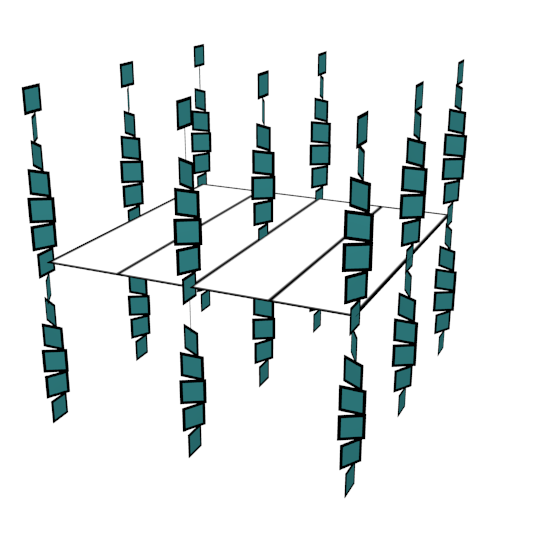
This example can be turned into a convex torus with Morse-Smale characteristic foliation by waving. The wave amplitude in the next picture ensures that one can see what is going on but the topological picture does not depend on it so that this transformation is really a small perturbation in smooth topology.

If you use a recent version of a decent web browser (Firefox 4 would do) and you have an accelerated graphics card, you may be able to play with an interactive version of the above picture (try moving around the mouse while holding various buttons to figure out how it works).

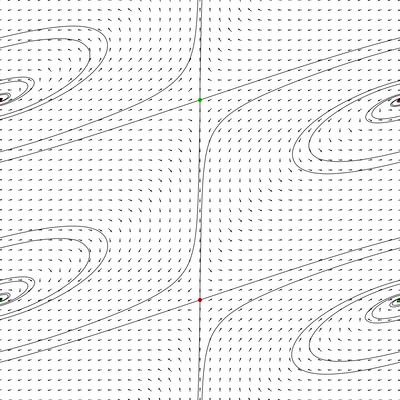
If we start with a linear foliation whose leaves are dense then we start by moving in slightly up or down to get back to the preceding situation.

Retrograde connections

The horizontal torus of the previous example was not convex because of its degenerate closed leaves. We now give an example a surface whose convexity is obstructed by a retrograde saddle connection (actually two of them). The central fiber of the picture is tangent both to the contact structure and to the surface. The surface and the contact structures rotates in the same direction along this fiber but the surface goes twice faster. So, compared to the surface, the contact structure rotates in the direction opposite to its rotation along Legendrian foliations. This is what causes retrograde connections. The lines drawn on the surfaces are separatrices of the two saddles. The following picture is a movie of unwrapped characteristic foliation in a neighborhood of this surface which appears as the middle one. One can see the switching behavior predicted by Giroux's crossing lemma.

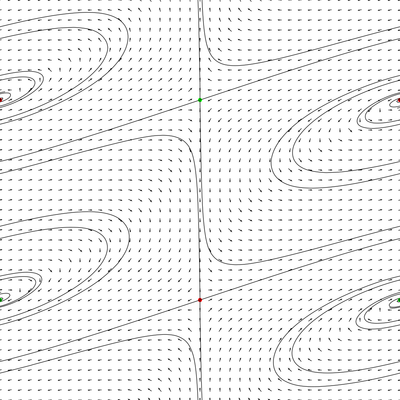
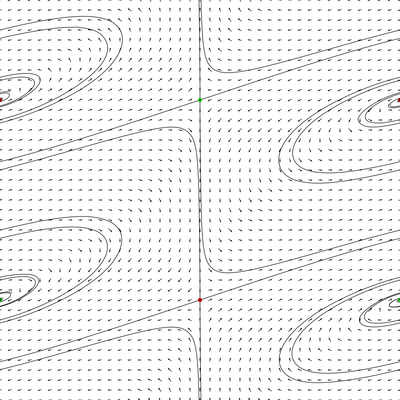
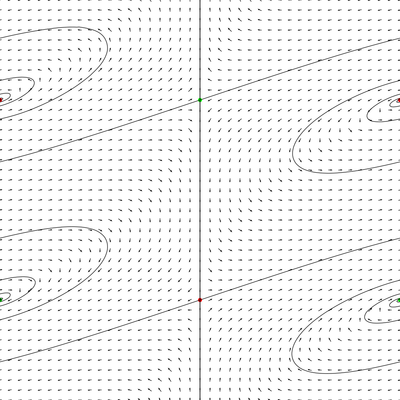
Realization lemma

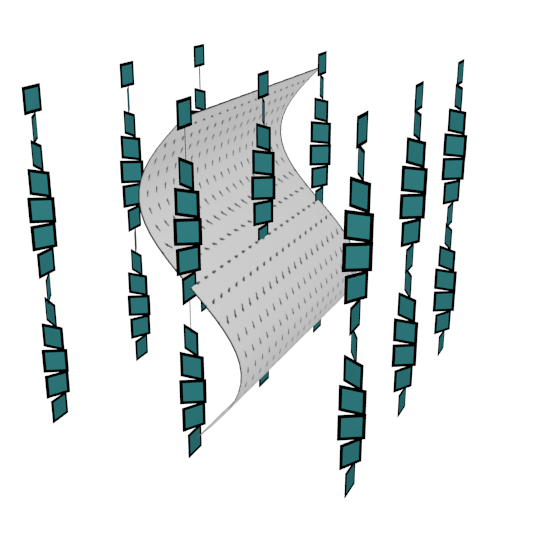
As an example of realization of foliations, we start with a perfectly vertical torus. Its characteristic foliation has two circles of singularities, there are horizontal. It is divided by horizontal circles sitting between the singularity circles. In the following picture we draw this foliation with a dashed dividing set and also a more generic foliation divided by the same set.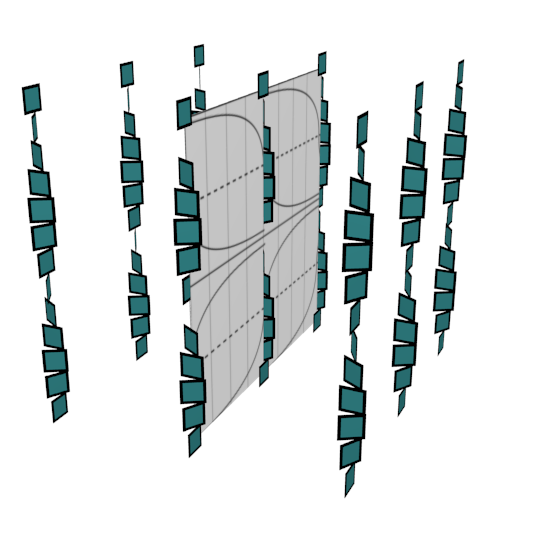 Giroux's realization lemma implies any neighborhood of our torus contains a torus realizing this generic foliation. Again it's a waving trick.

If you use a recent version of a decent web browser (Firefox 4 would do) and you have an accelerated graphics card, you may be able to play below with an of the above picture (try moving around the mouse while holding various buttons to figure out how it works).