Gallery
Click on pictures for a large version.
-
A lozenge tiling on a torus, in a gas phase:

-
A discrete loop model under current investigation, here captured on a torus:
-
Here is a Sage program for plotting amoebas and coamoebas of complex polynomials (written with the Jupyter notebook): amo_coamo.ipynb.
For example, a few amoebas coming from the eight-vertex-model:
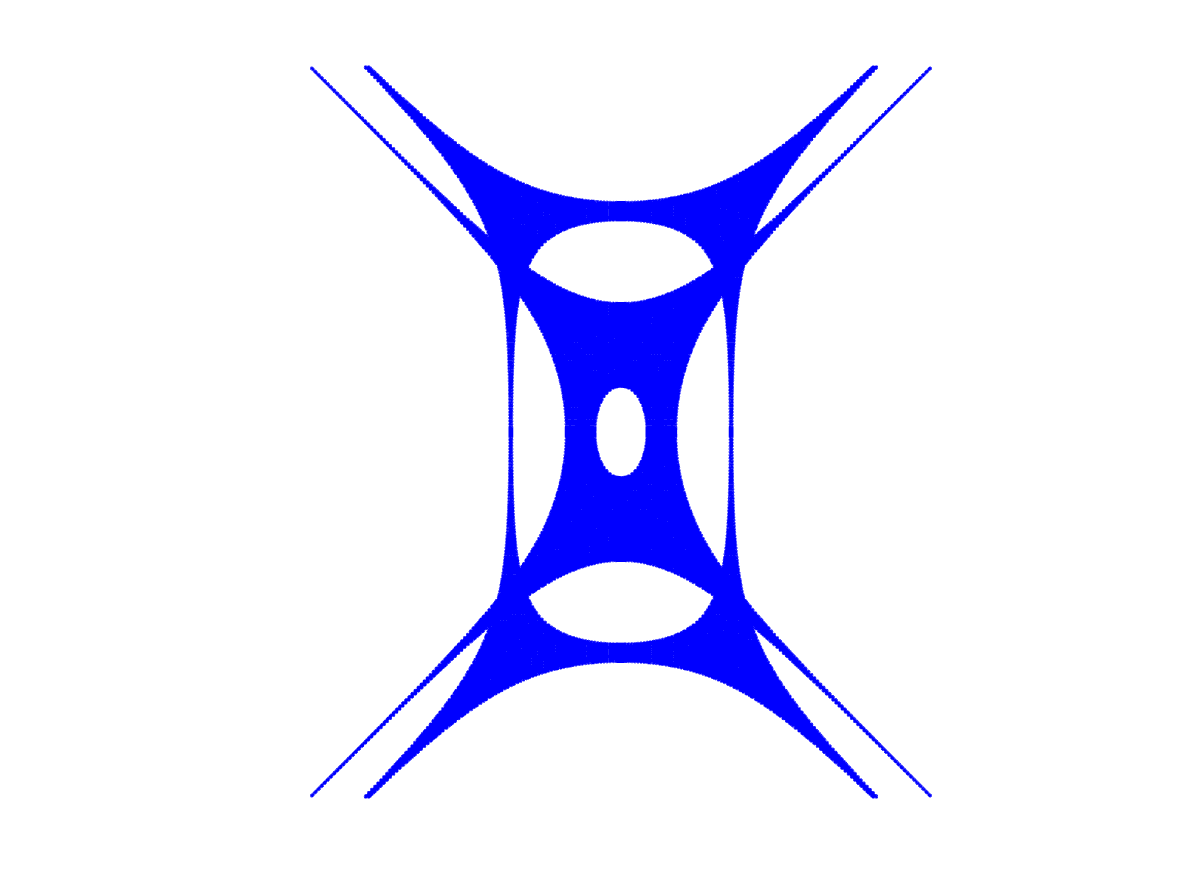


The first two amoebas correspond to "free-fermion" models and seem to be the superposition of more simple, Harnack curves. This fact is explained here.
-
Simulations of the loop model studied here, that exhibits a limit shape phenomenon:



If we let the size of the pile of cubes be constant while taking very big values for the weights, the measure concentrates on configurations of low energy, giving a "snowflake" phenomenon:



It is also possible to get an equivalent representation for cube groves as a limit:

-
Simulation of the s-embeddings defined by D. Chelkak, adapted to a the planar setting, using a large piece of the square lattice:
With critical weights (before and after applying an inversion)
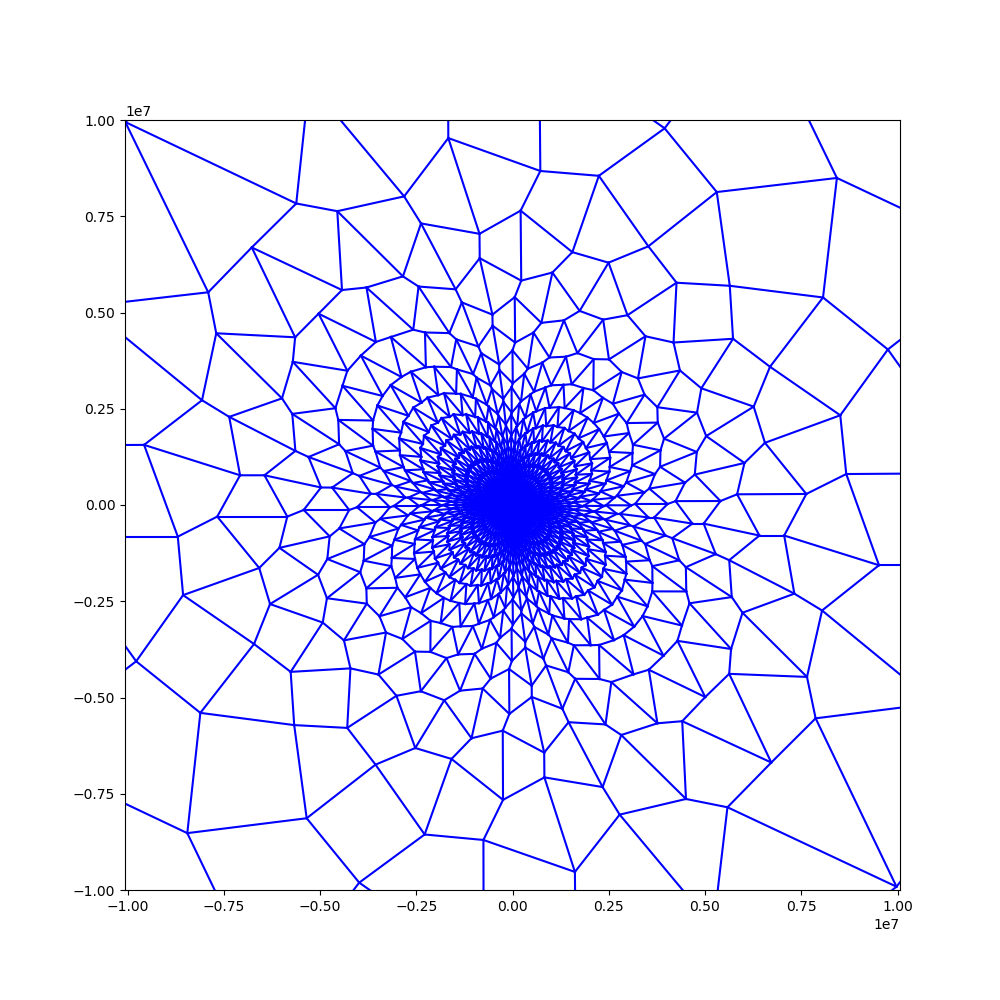
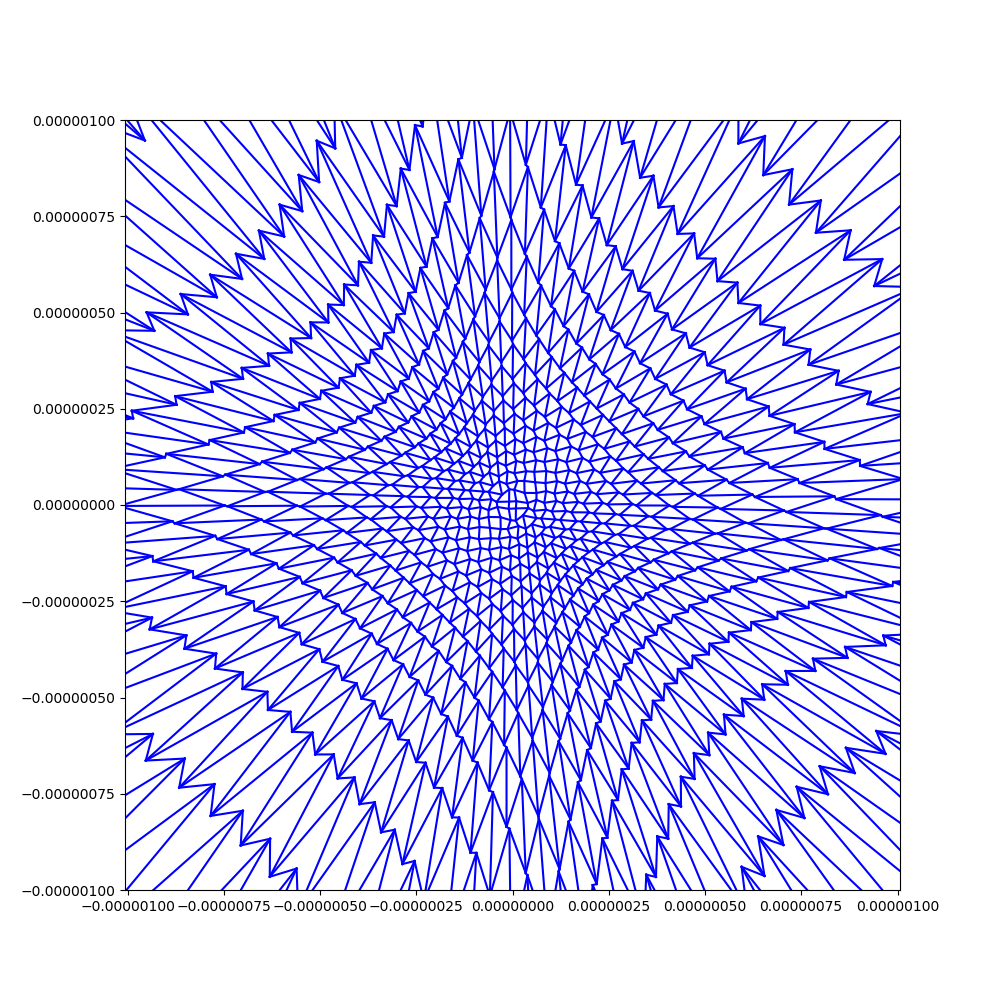
With sub-critical weights
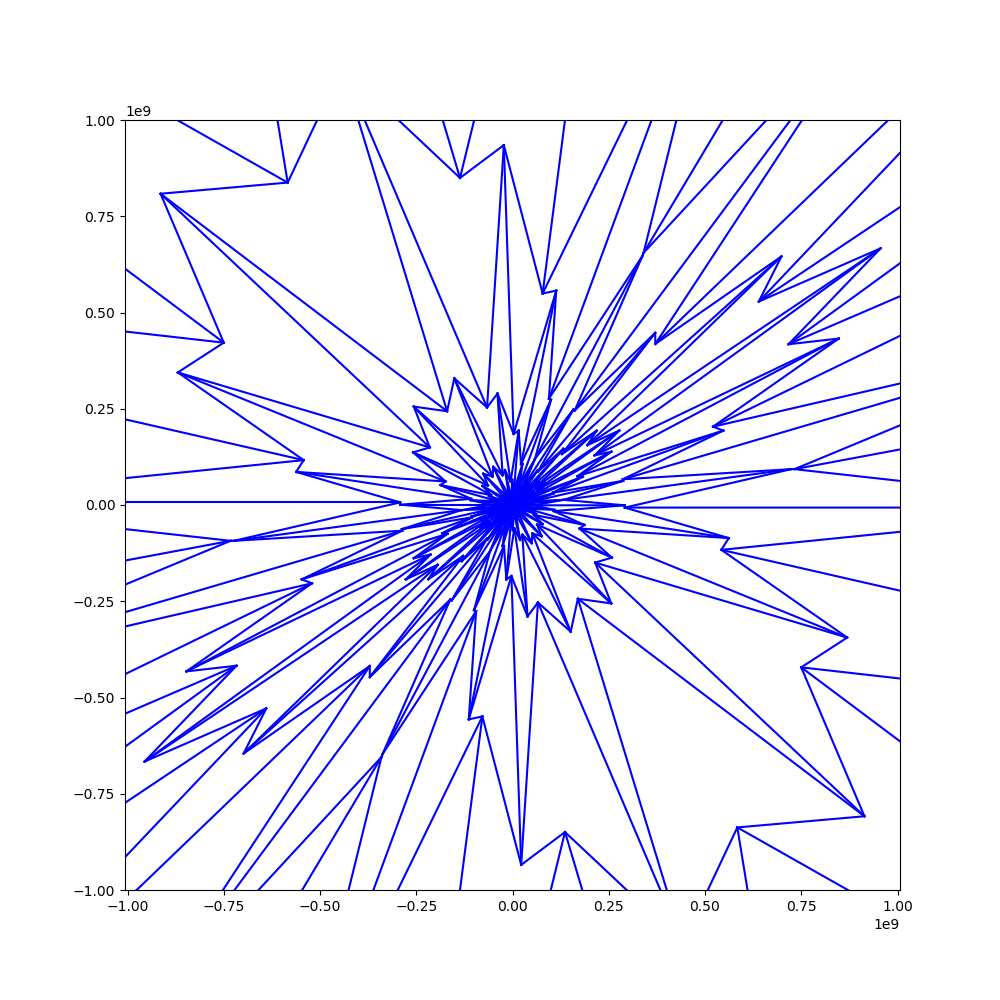
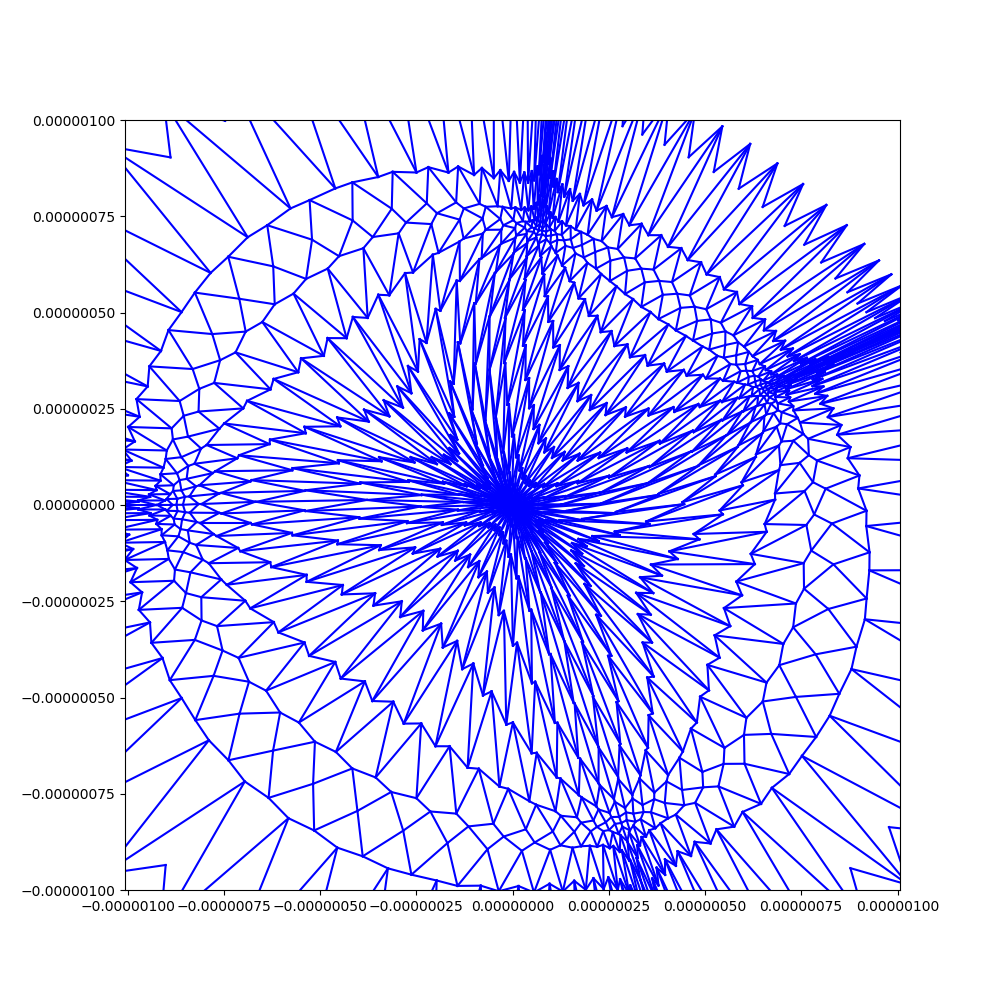
With super-critical weights