Mixing C r maps of the interval without maximal measure
Israel Journal of Math., 127, 253-277, 2002.
Abstract
We construct a C r transformation of the interval (or the torus)
which is topologically mixing but has no invariant measure of maximal
entropy.
Whereas the assumption o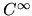f 
ensures existence of
maximal measures for an interval map, it shows we cannot weaken the
smoothness assumption.
We also compute the local entropy of the example.
Paper:
[arXiv:1901.00325]
[pdf]