For graph maps, one scrambled pair implies Li-Yorke chaos
Proceedings of the American Mathematical Society, 142, No. 6, 2087-2100, 2014.
Abstract
For a dynamical system (X,f), X being a compact metric space with metric d
and f being a continuous map from X to X, a set S included in X
is scrambled if every pair (x,y) of distinct points in S is scrambled,
i.e.,
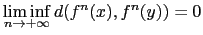 and
and
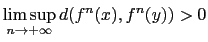 .
The system (X,f) is
Li-Yorke chaotic if it has an uncountable scrambled set. It is
known that, for interval and circle maps, the existence of a scrambled pair
implies Li-Yorke chaos, in fact the existence of a Cantor scrambled set.
We prove that the same result holds for graph maps.
We further show that on compact countable metric spaces
one scrambled pair implies the existence of an infinite scrambled set.
.
The system (X,f) is
Li-Yorke chaotic if it has an uncountable scrambled set. It is
known that, for interval and circle maps, the existence of a scrambled pair
implies Li-Yorke chaos, in fact the existence of a Cantor scrambled set.
We prove that the same result holds for graph maps.
We further show that on compact countable metric spaces
one scrambled pair implies the existence of an infinite scrambled set.
Paper: [arXiv:1205.3882]
[pdf (published paper)]