Papers/Preprints
Guillaume Blanc and Jonas Kahn PDF Published in
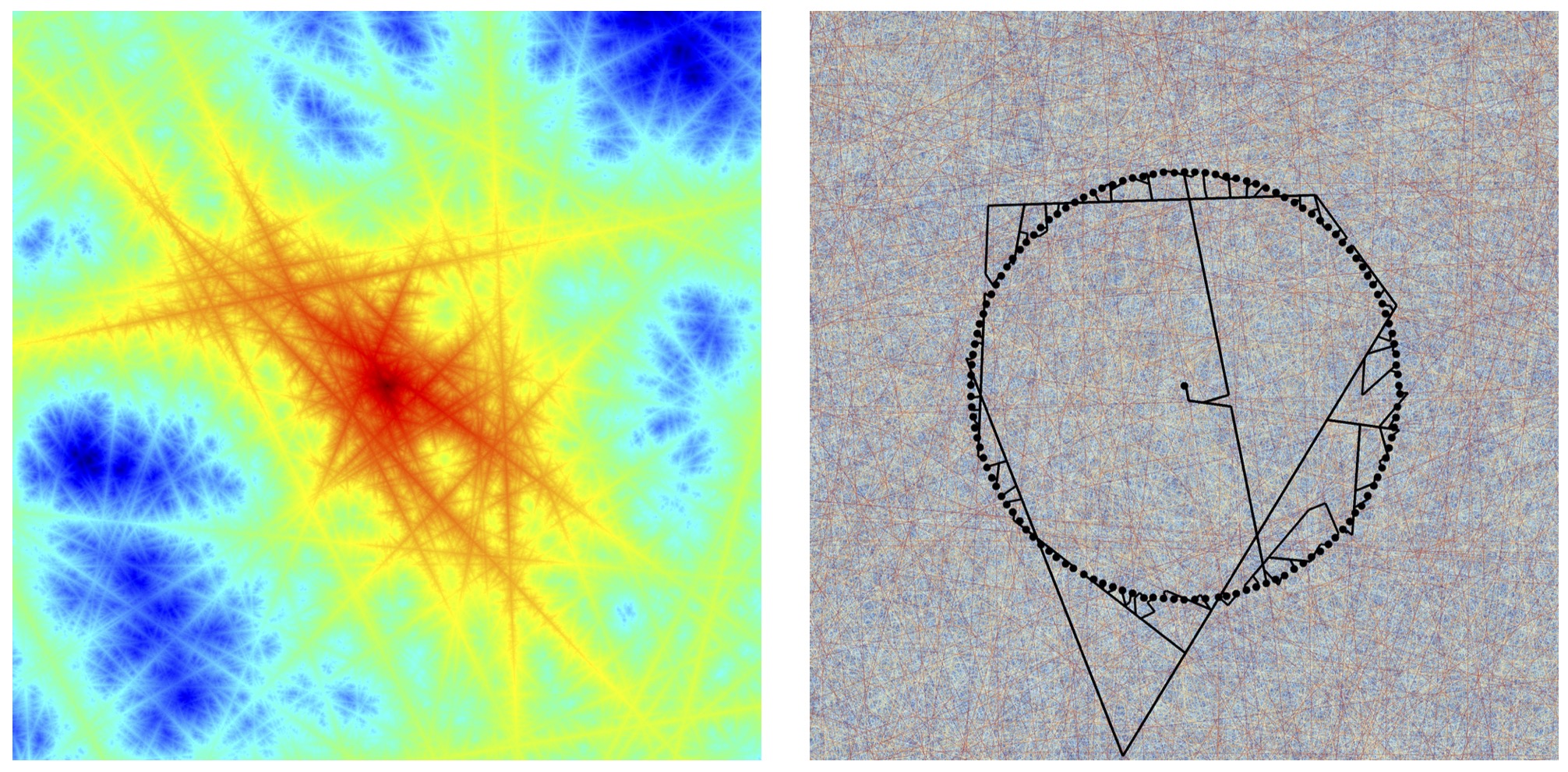
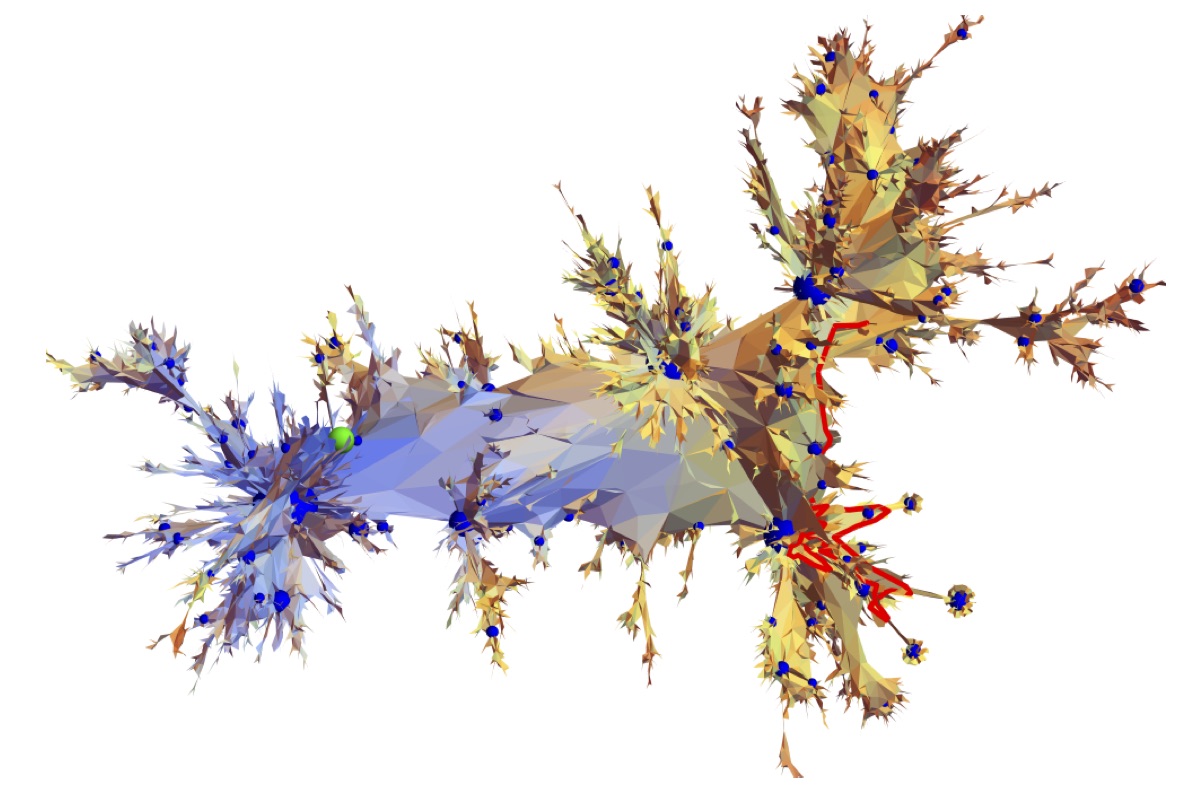
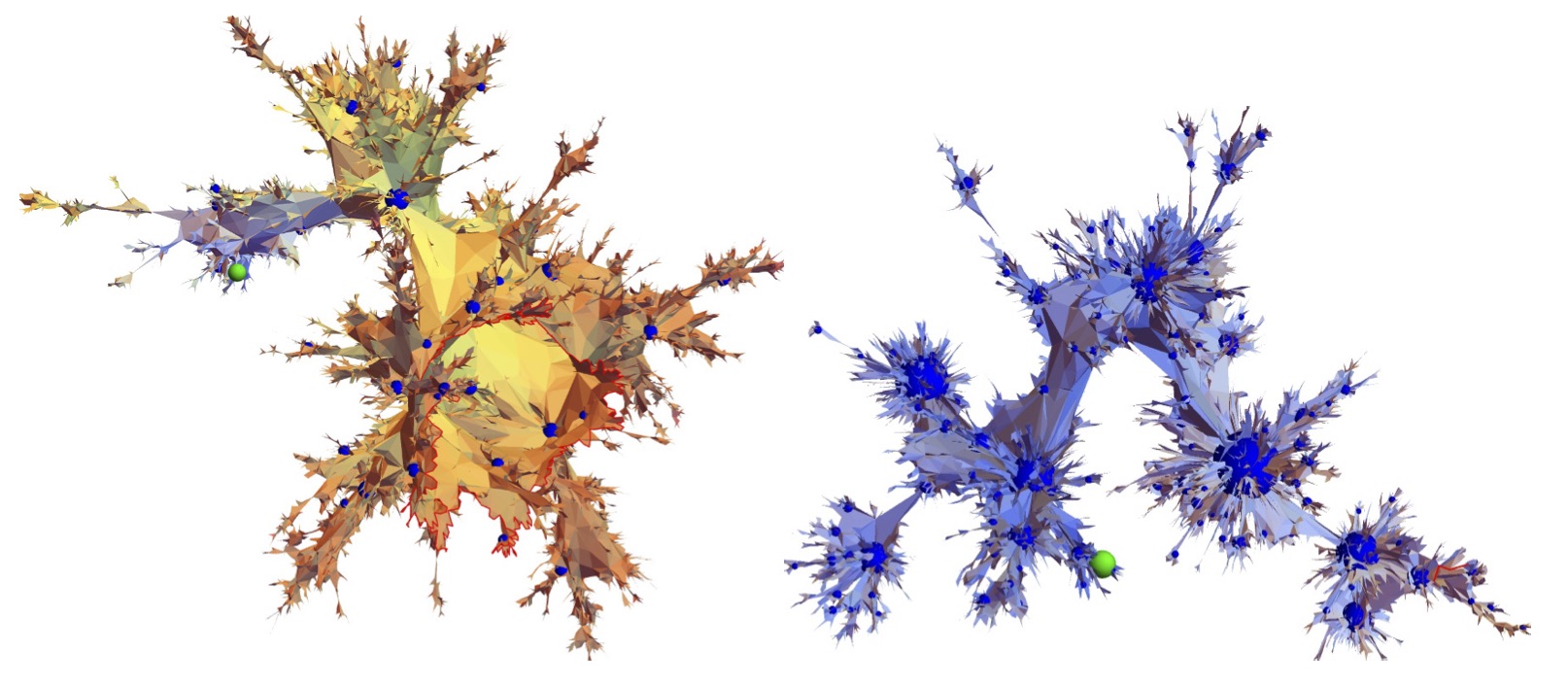
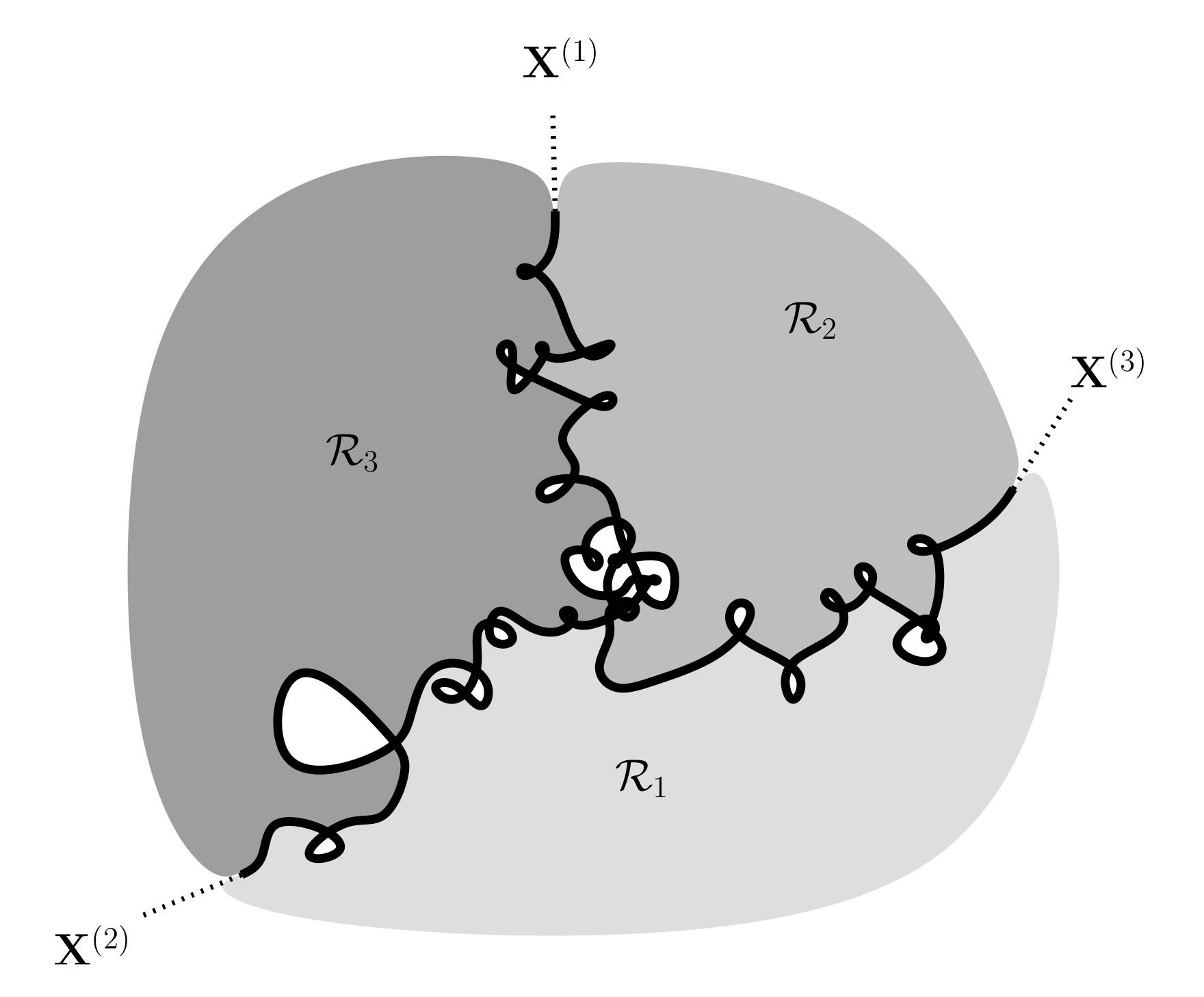
We study the structure of geodesics in the fractal random metric constructed by Kendall from a self-similar Poisson process of roads (i.e, lines with speed limits) in $\mathbb{R}^2$. In particular, we prove a conjecture of Kendall stating that geodesics do not pause en route, i.e, use roads of arbitrary small speed except at their endpoints. It follows that the geodesic frame of $( \mathbb{R}^2,T)$ is the set of points on roads. We also consider geodesic stars and hubs, and give a complete description of the local structure of geodesics around points on roads. Notably, we prove that leaving a road by driving off-road is never geodesic.

with David Aldous and Guillaume Blanc PDF Published in Annales Faculté des sciences de Toulouse
What distributions arise as the distribution of the distance between two typical points in some measured metric space? This seems to be a surprisingly subtle problem. We conjecture that every distribution with a density function whose support contains 0 does arise in this way, and give some partial results in that direction.
with Alessandra Caraceni and Robin Stephenson PDF Published in
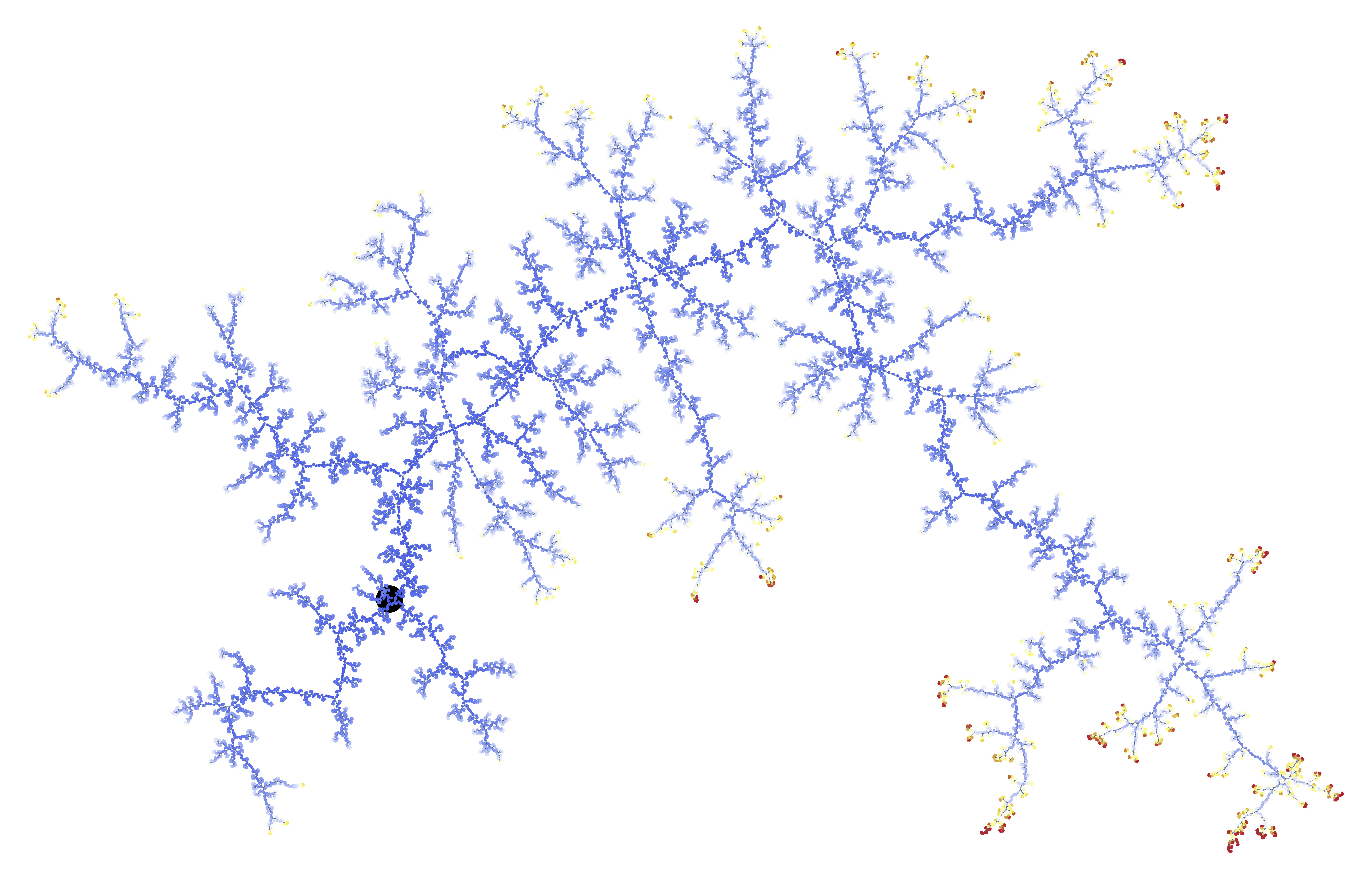
We study a model of random binary trees grown ``by the leaves" in the style of Luczak and Winkler. If $\tau_n$ is a uniform plane binary tree of size $n$, Luczak and Winkler, and later explicitly Caraceni and Stauffer, constructed a measure $\nu_{\tau_n}$ such that the tree obtained by adding a cherry on a leaf sampled according to $\nu_{\tau_n}$ is still uniformly distributed on the set of all plane binary trees with size $n+1$. It turns out that the measure $\nu_{\tau_n}$, which we call the leaf-growth measure, is noticeably different from the uniform measure on the leaves of the tree $\tau_n$. In fact we prove that as $n \to \infty$, with high probability it is almost entirely supported by a subset of only
$$ n^{3 ( 2 - \sqrt{3})+o(1)} \approx n^{0.8038...} \mbox{ leaves}.$$
In the continuous setting, we construct the scaling limit of this measure, which is a probability measure on the Brownian Continuum Random Tree supported by a fractal set of dimension $ 6 (2 - \sqrt{3})$. We also compute the full (discrete) multifractal spectrum. This work is a first step towards understanding the diffusion limit of the discrete leaf-growth procedure.

with Ariane Carrance and Jérome Casse PDF Published in
We introduce and study a model of plane random trees generalizing the famous Bienaymérome--Galton--Watson model but where births and deaths are locally correlated. More precisely, given a random variable $(B,H)$ with values in $ \{1,2,3,...\}^2$, given the state of the tree at some generation, the next generation is obtained (informally) by successively deleting $B$ individuals side-by-side and replacing them with $H$ new particles where the samplings are i.i.d. We prove that, in the critical case $ \mathbb{E}[B]= \mathbb{E}[H]$, and under a third moment condition on $B$ and $H$, the random trees coding the genealogy of the population model converges towards the Brownian Continuum Random Tree. Interestingly, our proof does not use the classical height process or the Lukasiewicz exploration, but rather the stochastic flow point of view introduced by Bertoin \& Le Gall.

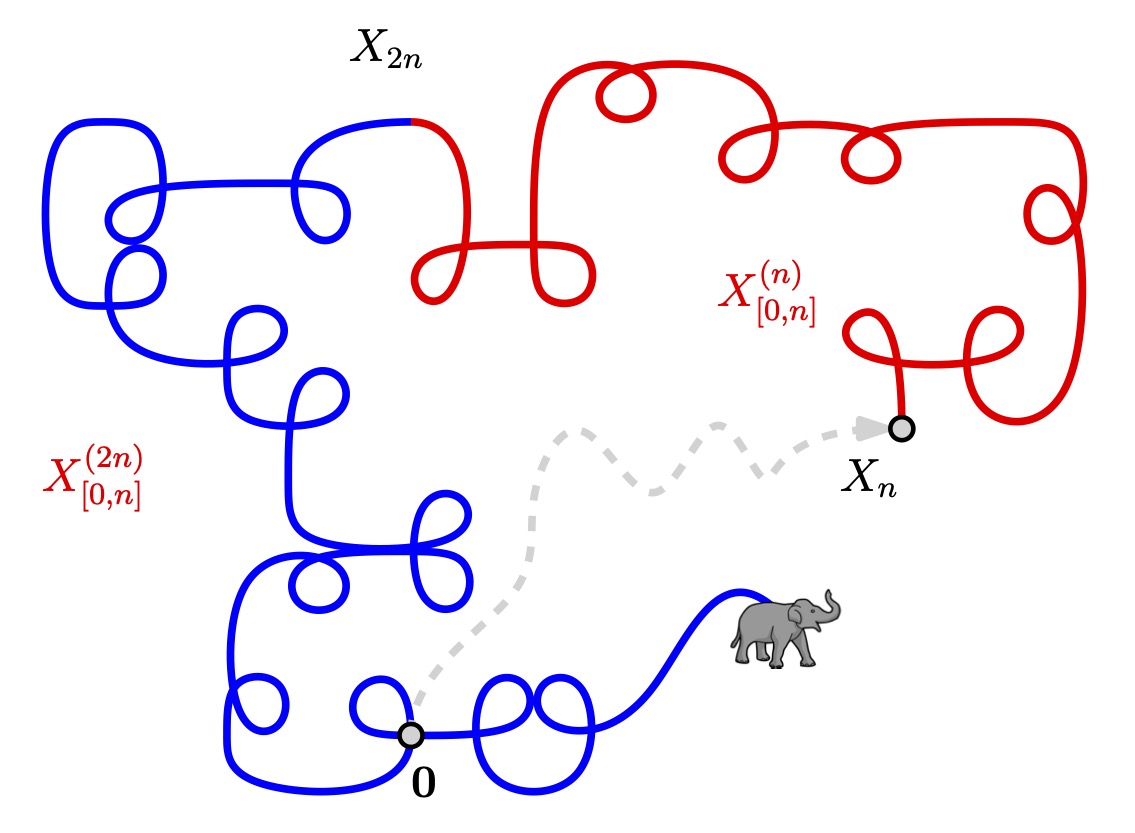
with Lucile Laulin PDF Published in CRAS
We give a short proof of the recurrence of the two-dimensional elephant random walk in the diffusive regime. This was recently established by Shuo Qin, but our proof only uses very rough comparison with the standard plane random walk. We hope that the method can be useful for other applications.

with Matteo D'Achille, Nathanael Enriquez, Russell Lyons and Meltem Unel PDF Published in Annals of Proba
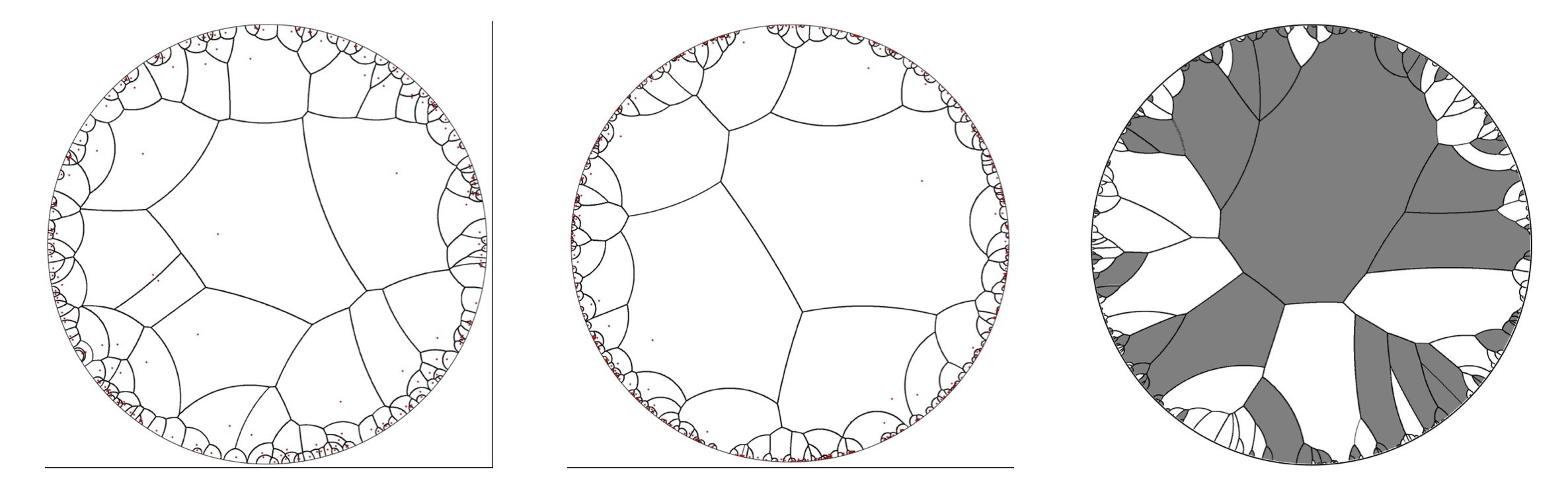
We study the limit in low intensity of Poisson-Voronoi tessellations in hyperbolic spaces $\mathbb{H}_d $ for $d \geq 2$. In contrast to the Euclidean setting, a limiting non-trivial ideal tessellation appears as the intensity tends to 0. The tessellation $ \mathrm{V}_d$ is a natural isometry-invariant (a.k.a. Mobius-invariant) decomposition of $\mathbb{H}_d $ into countably many infinite convex polytopes, each with a unique end. We study its basic properties, in particular the geometric features of its cells.
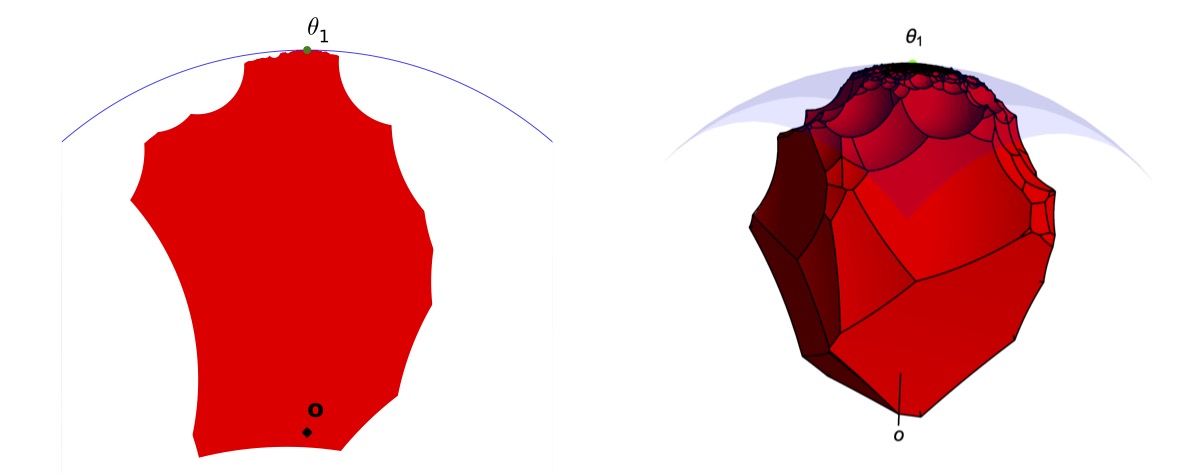

with Alice Contat, Perrine Lacroix, Etienne Lasalle and Vincent Rivoirard PDF Published in PTRF
We consider the problem of finding the initial vertex (Adam) in a Barab\'asi--Albert tree process $ (\mathrm{T}(n) : n \geq 1)$ at large times. More precisely, given $ \varepsilon>0$, one wants to output a subset $ \mathrm{P}_{ \varepsilon}(n)$ of vertices of $ \mathrm{T}(n)$ so that the initial vertex belongs to $ \mathrm{P}_ \varepsilon(n)$ with probability at least $1- \varepsilon$ when $n$ is large. It has been shown by Bubeck, Devroye \& Lugosi, refined later by Banerjee \& Huang, that one needs to output at least $ \varepsilon^{-1 + o(1)}$ and at most $\varepsilon^{-2 + o(1)}$ vertices to succeed. We prove that the exponent in the lower bound is sharp and the key idea is that Adam is either a ``large degree" vertex or is a neighbor of a ``large degree" vertex (Eve).


with Anne-Laure Basdevant, Guillaume Blanc and Arvind Singh PDF Published in ALEA
We study a model of random partitioning by nearest-neighbor coloring from Poisson rain, introduced independently by Aldous and Preater. Given two initial points in $[0,1]^d$ respectively colored in red and blue, we let independent uniformly random points fall in $[0,1]^d$, and upon arrival, each point takes the color of the nearest point fallen so far. We prove that the colored regions converge in the Hausdorff sense towards two random closed subsets whose intersection, the frontier, has Hausdorff dimension strictly between $(d-1)$ and $d$, thus answering a conjecture raised by Aldous. However, several topological properties of the frontier remain elusive.


with Thomas Budzinski and Alice Contat PDF Published in Annals of Applied Proba
We study the Karp--Sipser core of a random graph made of a configuration model with vertices of degree $1,2$ and $3$. This core is obtained by recursively removing the leaves as well as their unique neighbors in the graph. We settle a conjecture of Bauer & Golinelli and prove that at criticality, the Karp--Sipser core has size $ \approx \mathrm{Cst} \cdot \vartheta^{-2} \cdot n^{3/5}$ where $\vartheta$ is the hitting time of the curve $t \mapsto \frac{1}{t^{2}}$ by a linear Brownian motion started at $0$. Our proof relies on a detailed multi-scale analysis of the Markov chain associated to Karp-Sipser leaf-removal algorithm close to its extinction time.

Published in CRAS PDF
We introduce a variant of the Erdös--Rényi random graph where the number of vertices is random and follows a Poisson law. A very simple Markov property of the model entails that the Lukasiewicz exploration is made of independent Poisson increments. Using a vanilla Poisson counting process, this enables us to give very short proofs of classical results such as the phase transition for the giant component or the connectedness for the standard Erdös--Rényi model.
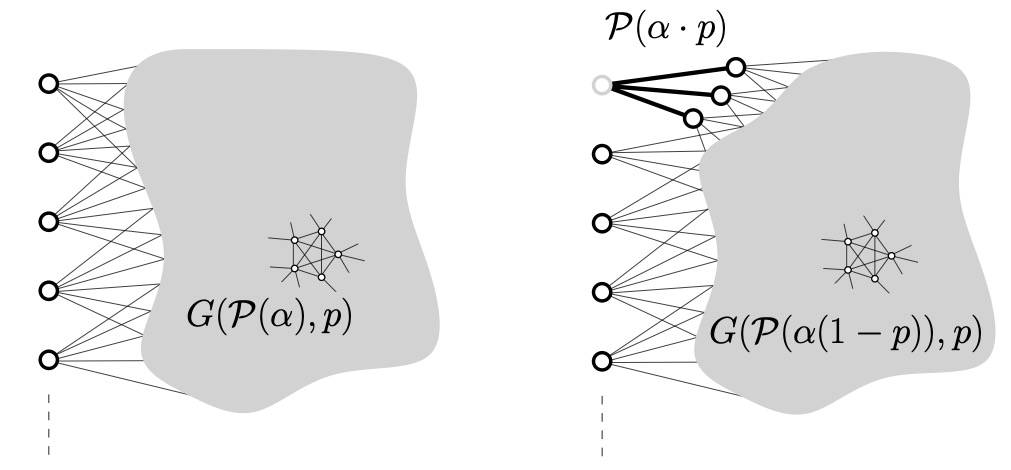

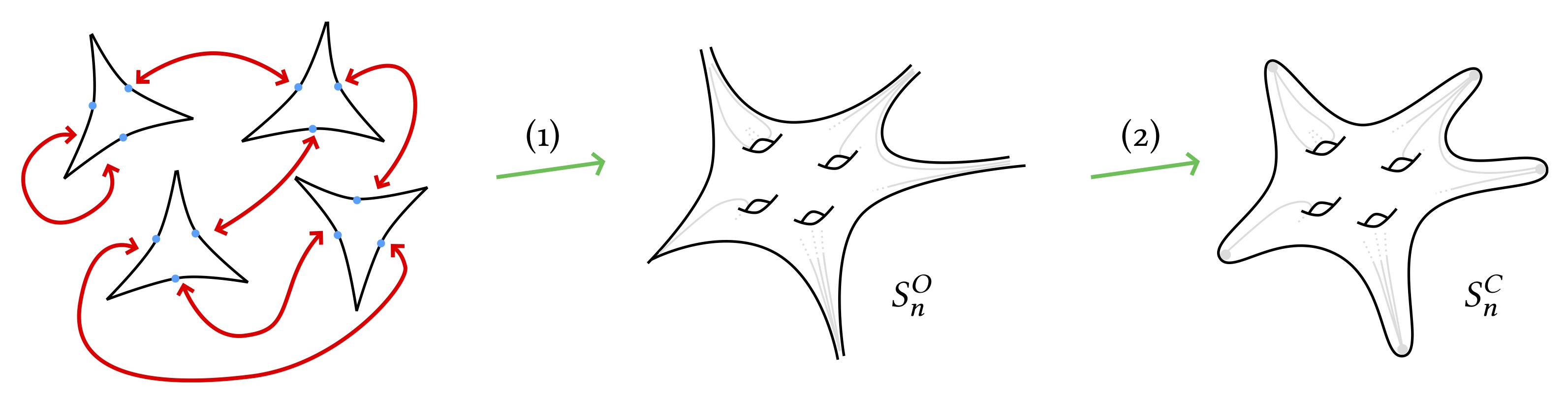
with Thomas Budzinski and Bram Petri PDF Published in Inventiones Mathematicae
It is a well-known result due to Bollobas that the maximal Cheeger constant of large d-regular graphs cannot be close to the Cheeger constant of the d-regular tree. We prove analogously that the Cheeger constant of closed hyperbolic surfaces of large genus is bounded from above by $2/pi \approx 0.63...$ which is strictly less than the Cheeger constant of the hyperbolic plane. The proof uses a random construction based on a Poisson--Voronoi tessellation of the surface with a vanishing intensity.

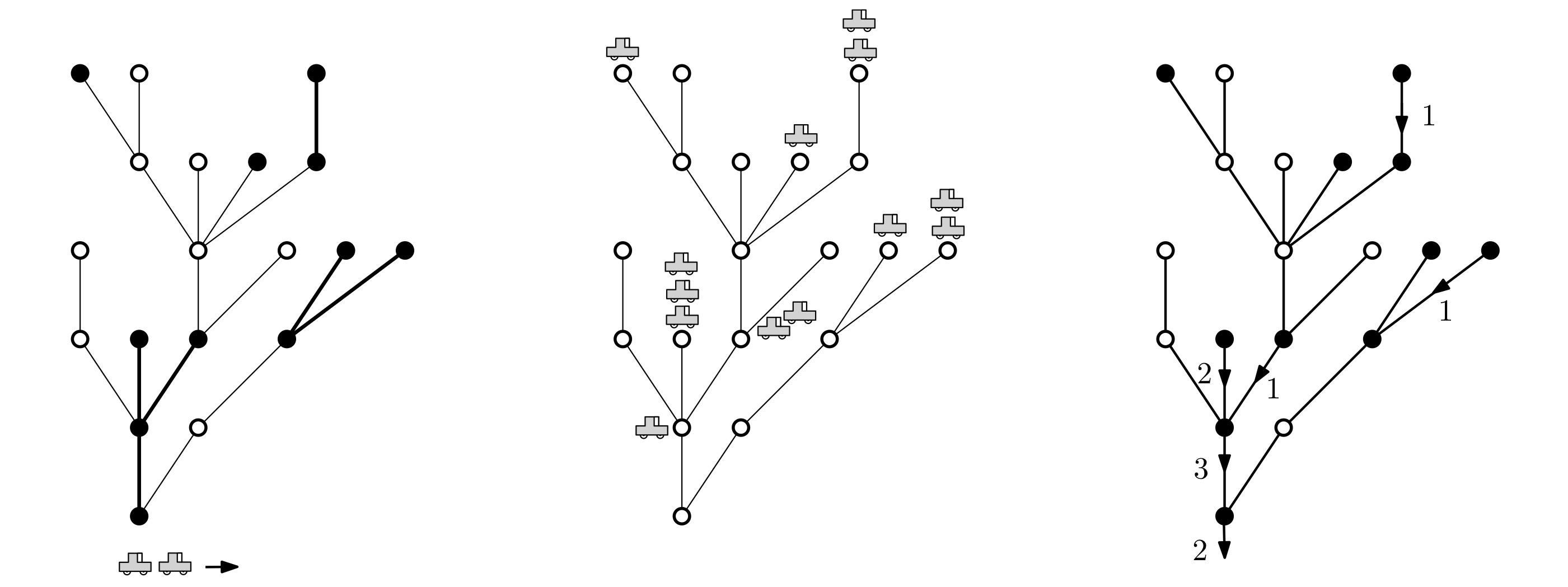
with David Aldous, Alice Contat and Oliver Hénard PDF Published in Probability Theory and Related Fields
Let $(A_u : u \min \mathbb{B})$ be i.i.d.~non-negative integers that we interpret as car arrivals on the vertices of the full binary tree $\mathbb{B}$. Each car tries to park on its arrival node, but if it is already occupied, it drives towards the root and parks on the first available spot. It is known that the parking process on $\mathbb{B}$ exhibits a phase transition in the sense that either a finite number of cars do not manage to park in expectation (subcritical regime) or all vertices of the tree contain a car and infinitely many cars do not manage to park (supercritical regime). We characterize those regimes in terms of the law of $A$ in an explicit way. We also study in detail the critical regime as well as the phase transition which turns out to be "discontinuous".
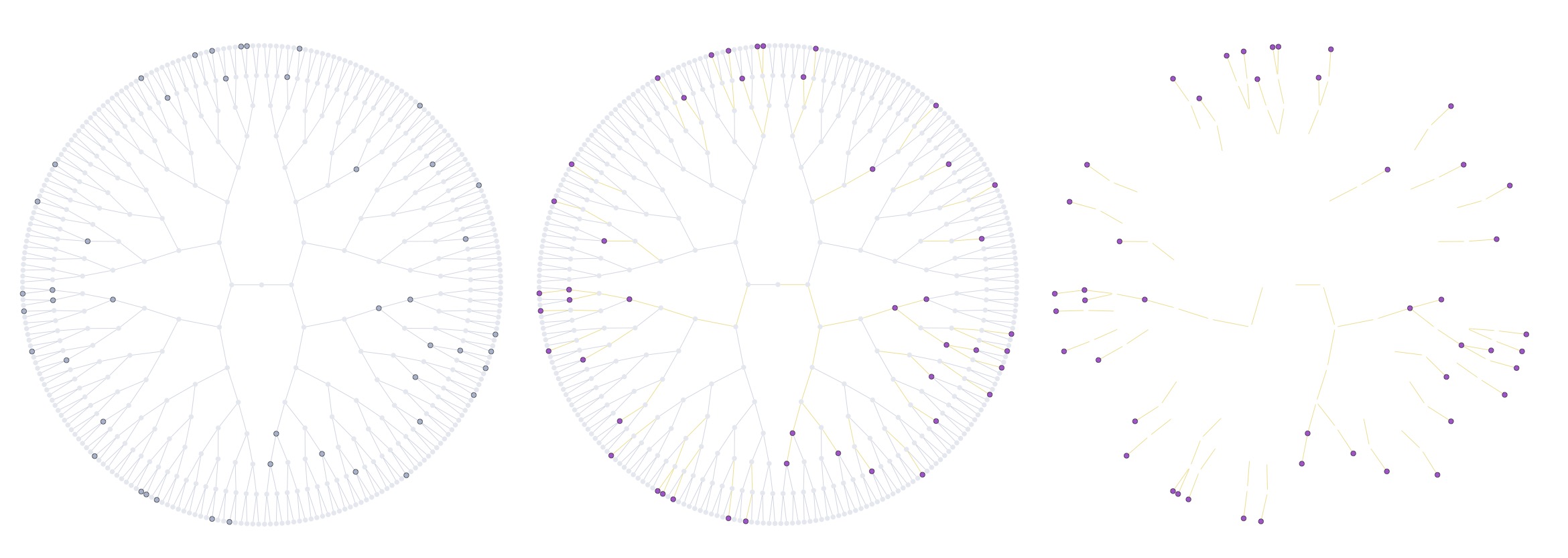

with Igor Kortchemski and Cyril Marzouk PDF Published in Journal de l'Ecole Polytechnique
We investigate the structure of large uniform random maps with $n$ edges, $\mathrm{f}_n$ faces, and with genus $\mathrm{g}_n$ in the so-called sparse case, where the ratio between the number vertices and edges tends to $1$. We focus on two regimes: the planar case $(\mathrm{f}_n, 2\mathrm{g}_n) = (\mathrm{s}_n, 0)$ and the unicellular case with moderate genus $(\mathrm{f}_n, 2 \mathrm{g}_n) = (1, \mathrm{s}_n-1)$, both when $1 \ll \mathrm{s}_n \ll n$. Albeit different at first sight, these two models can be treated in a unified way using a probabilistic version of the classical core--kernel decomposition. In particular, we show that the number of edges of the core of such maps, obtained by iteratively removing degree $1$ vertices, is concentrated around $\sqrt{n \mathrm{s}_{n}}$. Further, their kernel, obtained by contracting the vertices of the core with degree $2$, is such that the sum of the degree of its vertices exceeds that of a trivalent map by a term of order $\sqrt{\mathrm{s}_{n}^{3}/n}$; in particular they are trivalent with high probability when $\mathrm{s}_{n} \ll n^{1/3}$. This enables us to identify a mesoscopic scale $\sqrt{n/\mathrm{s}_n}$ at which the scaling limits of these random maps can be seen as the local limit of their kernels, which is the dual of the UIPT in the planar case and the infinite three-regular tree in the unicellular case, where each edge is replaced by an independent (biased) Brownian tree with two marked points.
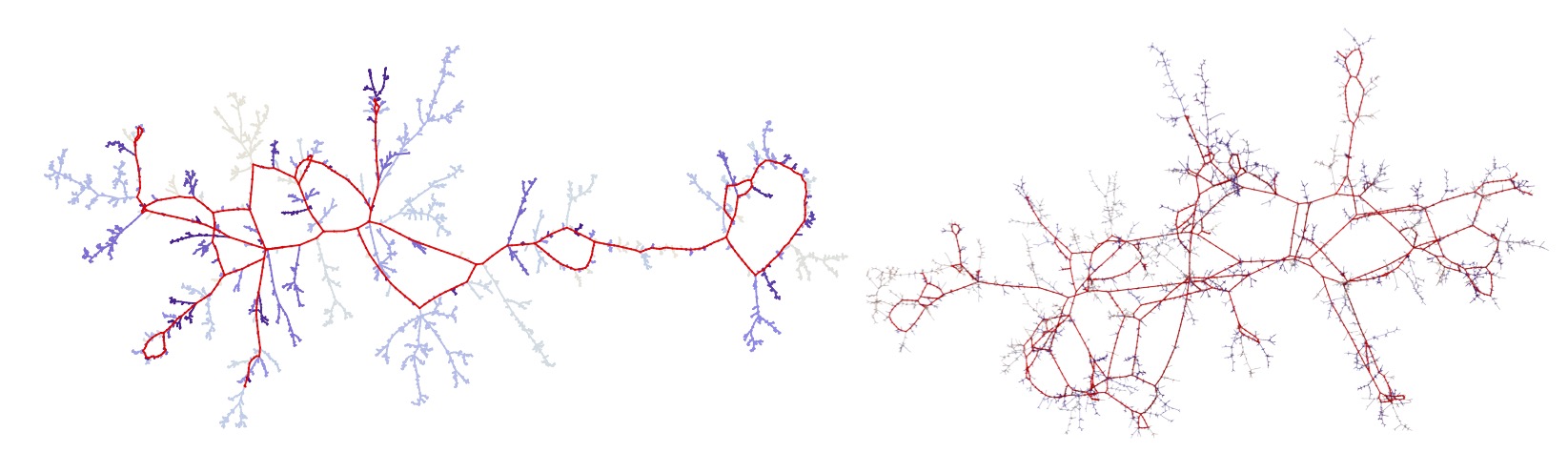

with Alice Contat PDF Published in Annals of Probability
Consider a uniform rooted Cayley tree $T_n$ with $n$ vertices and let m cars arrive sequentially, independently, and uniformly on its vertices. Each car tries to park on its arrival node, and if the spot is already occupied, it drives towards the root of the tree and parks as soon as possible. Lackner & Panholzer (arXiv:1504.04972) established a phase transition for this process when $m\approx n/2$. In this work, we couple this model with a variant of the classical Erdös-Rényi random graph process. This enables us to describe the phase transition for the size of the components of parked cars using a modification of the multiplicative coalescent which we name the frozen multiplicative coalescent. The geometry of critical parked clusters is also studied. Those trees are very different from Bienaymé-Galton-Watson trees and should converge towards the growth-fragmentation trees canonically associated to the $3/2$-stable process that already appeared in the study of random planar maps
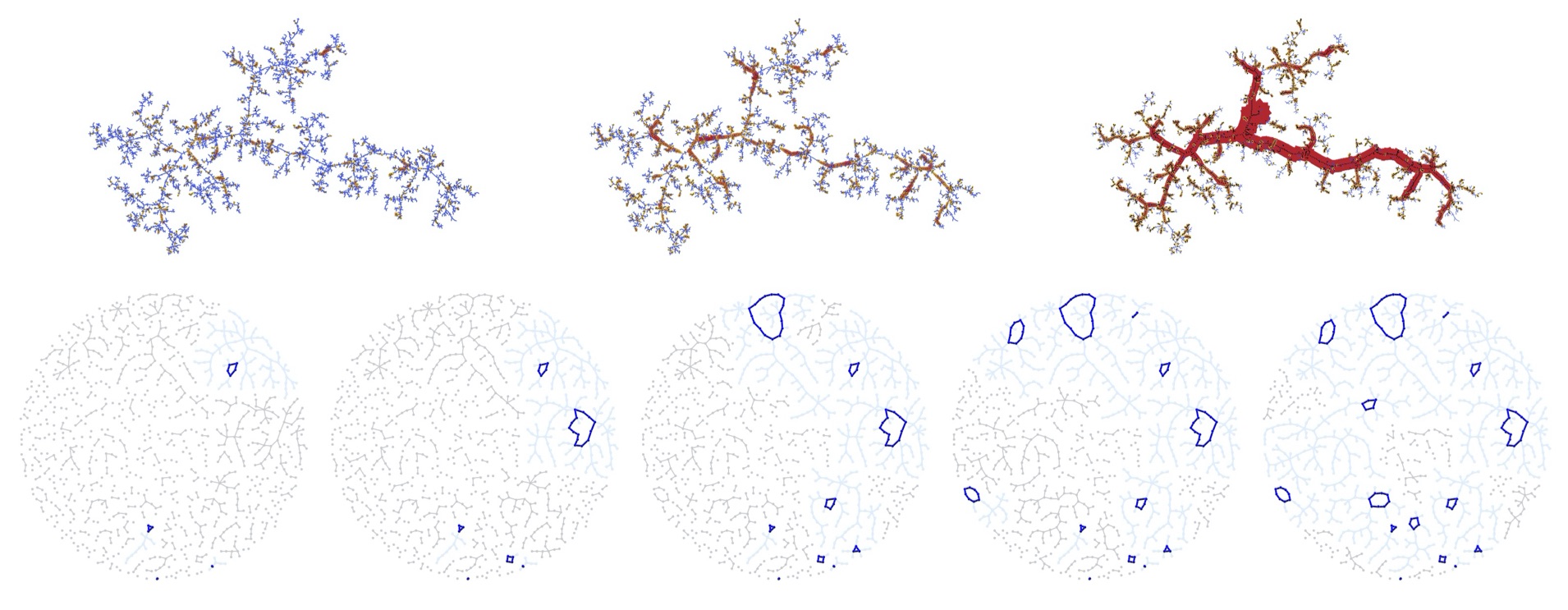

with Jérémie Bettinelli, Luis Fredes and Avelio Sepulveda PDF
Published in Annales IHP Proba/Stats
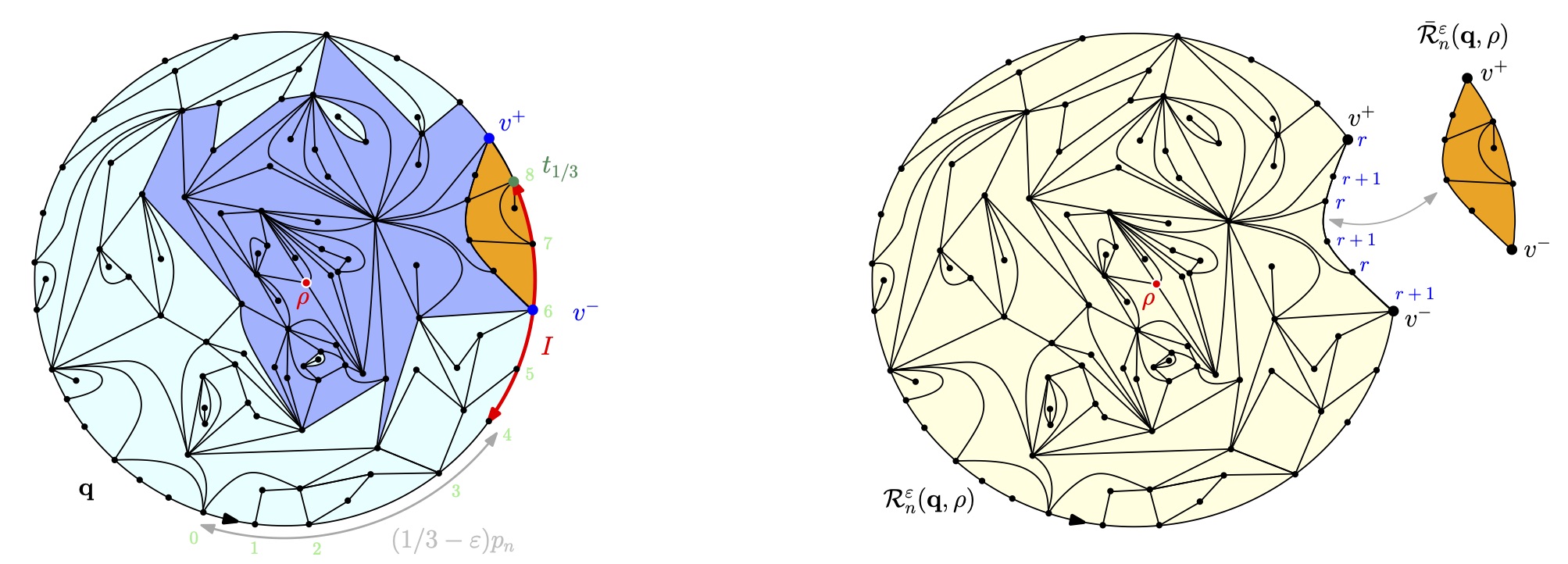
The main purpose of this work is to provide a framework for proving that, given a family of random maps known to converge in the Gromov--Hausdorff sense, then some (suitable) conditional families of random maps converge to the same limit. As a proof of concept, we show that quadrangulations with a simple boundary converge to the Brownian disk. More precisely, we fix a sequence $(p_n)$ of even positive integers with $p_n\sim 2 \alpha \sqrt{2n}$ for some $\alpha \in (0,\infty)$. Then, for the Gromov--Hausdorff topology, a quadrangulation with a simple boundary uniformly sampled among those with n inner faces and boundary length $p_n$ weakly converges, in the usual scaling $n^{-1/4}$, toward the Brownian disk of perimeter $3 \alpha$.

with Jérome Casse PDF Published in Confluentes Mathematici
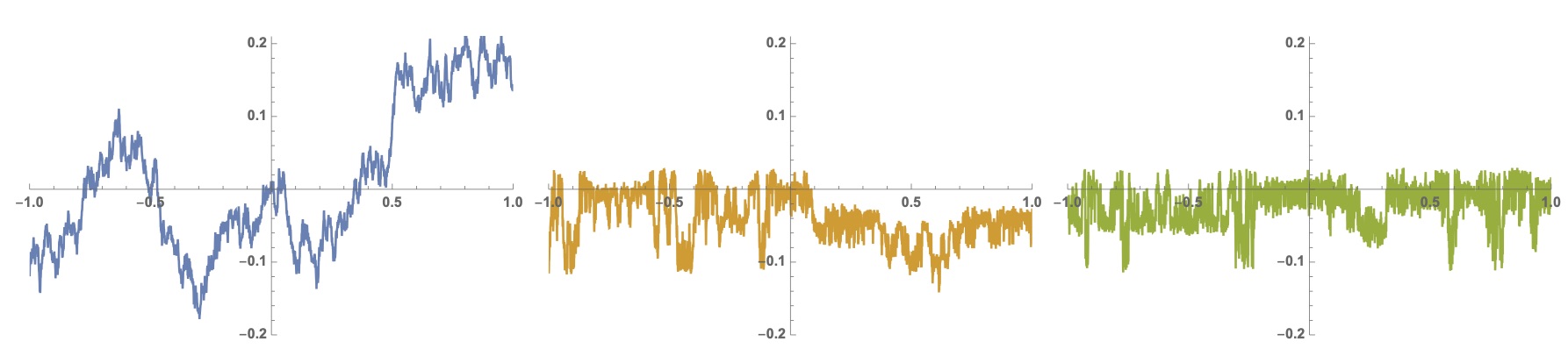
We show that the construction of a random continuum $\mathcal{C}$ from independent two-sided Brownian motions as considered in arXiv:2004.01367 almost surely yields a non-degenerate indecomposable but not-hereditary indecomposable continuum. In particular $\mathcal{C}$ is (unfortunately) not the pseudo-arc.

with Olivier Hénard PDF Published in Discrete Analysis
We establish a phase transition for the parking process on critical Galton--Watson trees. In this model, a random number of cars with mean m and variance $\sigma^2$ arrive independently on the vertices of a critical Galton--Watson tree with finite variance $\Sigma^2$ conditioned to be large. The cars go down the tree and try to park on empty vertices as soon as possible. We show a phase transition depending on
$$ \Theta:=(1-m)^2 -\Sigma^2(\sigma^2+m^2-m).$$
Specifically, if $\Theta>0$, then most cars will manage to park, whereas if $\Theta<0$ then a positive fraction of the cars will not find a spot and exit the tree through the root. This confirms a conjecture of Goldschmidt and Przykucki.

with Jakob Bjornberg and Sigurdur Orn Stefánsson PDF Published in Annals of Probability
We introduce a new familiy of random compact metric spaces $ \mathcal{S}_\alpha$, $\alpha \in (1,2)$ which we call stable shredded spheres. They are constructed from excursions of $\alpha$-stable Lévy processes on $[0,1]$ possessing no negative jumps. Informally, viewing the graph of the Lévy excursion in the plane, each jump of the process is "cut open" and replaced by a circle and then all points on the graph at equal height which are not separated by a jump are identified. We show that the shredded spheres arise as scaling limits of models of causal random planar maps with large faces which have been studied in the physics literature. We also establish that their Hausdorff dimension is almost surely equal to $\alpha$. Point identification in the shredded spheres is intimately connected to the presence of decrease points in stable spectrally positive Lévy processes as studied by Bertoin in the 90's..

with Thomas Budzinski and Bram Petri PDF Published in
We determine the asymptotic growth rate of the diameter of the random hyperbolic surfaces constructed by Brooks and Makover. This model consists of a uniform gluing of $2n$ hyperbolic ideal triangles along their sides followed by a compactification to get a random hyperbolic surface of genus roughly $n/2$. We show that the diameter of those random surfaces is asymptotic to $2\log n$ in probability as $n \to \infty$.

with Cyril Marzouk PDF Published in
The infinite discrete stable Boltzmann maps are generalisations of the well-known Uniform Infinite Planar Quadrangulation in the case where large degree faces are allowed. We show that the simple random walk on these random lattices is always subdiffusive with exponent less than $1/3$. Our method is based on stationarity and geometric estimates obtained via the peeling process which are of own interest.

with Thomas Budzinski and Bram Petri PDF Published in Duke
We prove that the minimal diameter of a hyperbolic compact orientable surface of genus $g$ is asymptotic to $\log g$ as $g \to \infty$. The proof relies on a random construction, which we analyse using lattice point counting theory and the exploration of random trivalent graphs.

with Timothy Budd PDF Published in
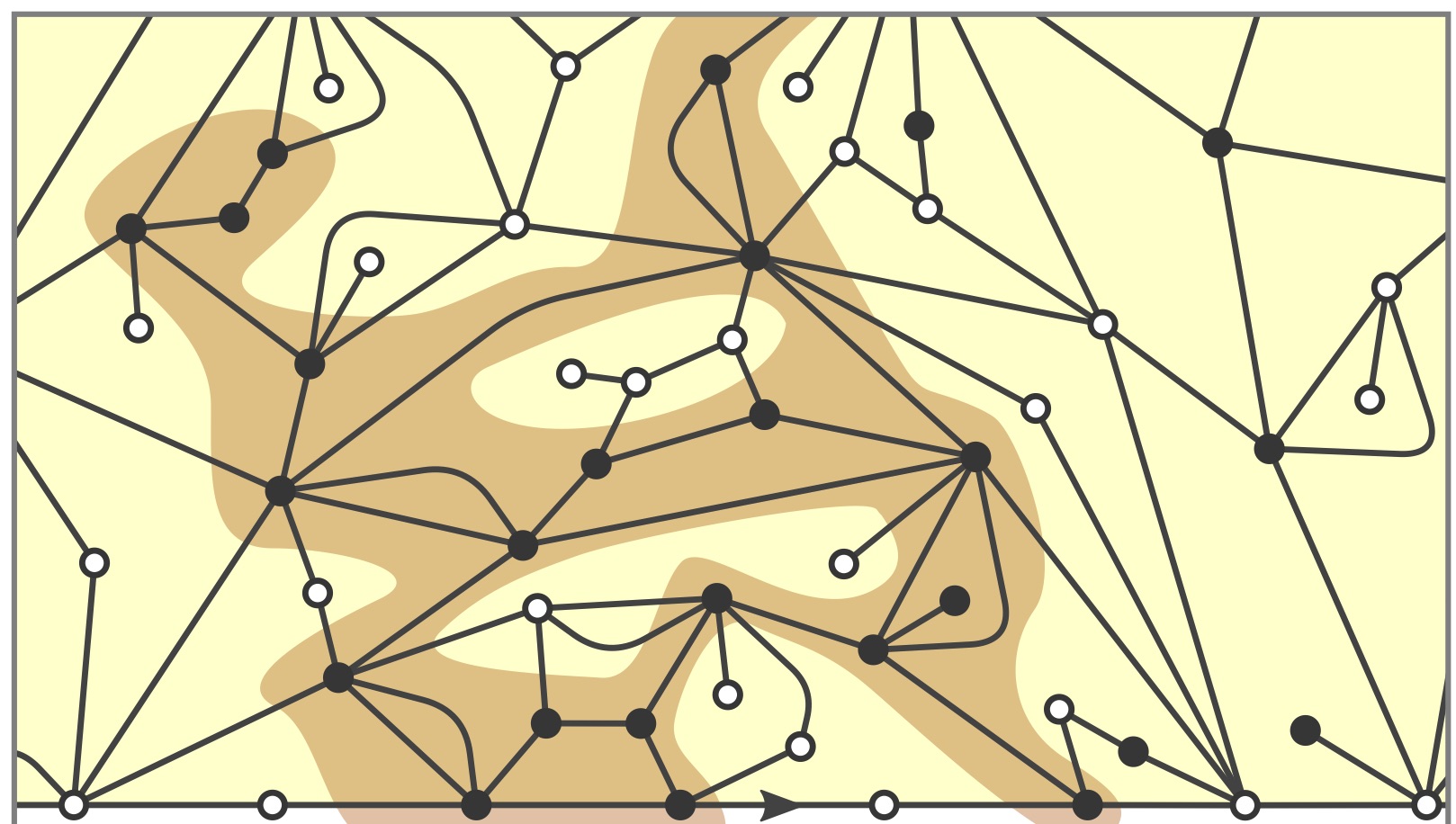
The peeling process, which describes a step-by-step exploration of a planar map, has been instrumental in addressing percolation problems on random infinite planar maps. Bond and face percolation on maps with faces of arbitrary degree are conveniently studied via so-called lazy-peeling explorations. During such explorations distinct vertices on the exploration contour may at later stage be identified, making the process less suited to the study of site percolation. To tackle this situation and to explicitly identify site-percolation thresholds, we come back to the alternative "simple" peeling exploration of Angel and uncover deep relations with the lazy-peeling process. Along the way we define and study the random Boltzmann map of the half-plane with a simple boundary for an arbitrary critical weight sequence. Its construction is nontrivial especially in the "dense regime" where the half-planar random Boltzmann map does not possess an infinite simple core.

with Jean Bertoin and Igor Kortchemski PDF Published in
The genealogical structure of self-similar growth-fragmentations can be described in terms of a branching random walk. The so-called intrinsic area A arises in this setting as the terminal value of a remarkable additive martingale. Motivated by connections with some models of random planar geometry, the purpose of this work is to investigate the effect of conditioning a self-similar growth-fragmentation on its intrinsic area. The distribution of A satisfies a useful smoothing transform which enables us to establish the existence of a regular density a and to determine the asymptotic behavior of $a(r)$ as $r \to \infty$ (this can be seen as a local version of Kesten-Grincevicius-Goldie theorem's for random affine fixed point equations in a particular setting). In turn, this yields a family of martingales from which the formal conditioning on $A=r$ can be realized by probability tilting. We point at a limit theorem for the conditional distribution given $A=r$ as $r \to \infty$, and also observe that such conditioning still makes sense under the so-called canonical measure for which the growth-fragmentation starts from 0
with Cyril Marzouk PDF Published in Bull. Soc. Math. France
The infinite discrete stable Boltzmann maps are "heavy-tailed" generalisations of the well-known Uniform Infinite Planar Quadrangulation. Very efficient tools to study these objects are Markovian step-by-step explorations of the lattice called peeling processes. Such a process depends on an algorithm which selects at each step the next edge where the exploration continues. We prove here that, whatever this algorithm, a peeling process always reveals about the same portion of the map, thus growing roughly metric balls. Applied to well-designed algorithms, this easily enables us to compare distances in the map and in its dual, as well as to control the so-called pioneer points of the simple random walk, both on the map and on its dual.

with Thomas Budzinski and Bram Petri PDF Published in Elec. J. Combinatorics
Starting from an arbitrary sequence of polygons whose total perimeter is $2n$, we can build an (oriented) surface by pairing their sides in a uniform fashion. Chmutov & Pittel have shown that, regardless of the configuration of polygons we started with, the degree sequence of the graph obtained this way is remarkably constant in total variation distance and converges towards a Poisson--Dirichlet partition as $n \to \infty$. We actually show that several other geometric properties of the graph are universal. En route we provide an alternative proof of a weak version of the result of Chmutov & Pittel using probabilistic techniques and related to the circle of ideas around the peeling process of random planar maps. At this occasion we also fill a gap in the existing literature by surveying the properties of a uniform random map with $n$ edges. In particular we show that the diameter of a random map with $n$ edges converges in law towards a random variable taking only values in $\{2,3\}$.

with Laurent Ménard PDF Published in Annales Henri Lebesgue
We prove that geodesic rays in the Uniform Infinite Planar Triangulation (UIPT) coalesce in a strong sense using the skeleton decomposition of random triangulations discovered by Krikun. This implies the existence of a unique horofunction measuring distances from infinity in the UIPT. We then use this horofunction to define the skeleton ``seen from infinity'' of the UIPT and relate it to a simple Galton--Watson tree conditioned to survive, giving a new and particularly simple construction of the UIPT. Scaling limits of perimeters and volumes of horohulls within this new decomposition are also derived, as well as a new proof of the $2$-point function formula for random triangulations in the scaling limit due to Ambjørn and Watabiki.

with Loïc Richier PDF Published in Annales Inst. Fourier
We discuss duality properties of critical Boltzmann planar maps such that the degree of a typical face is in the domain of attraction of a stable distribution with parameter $\alpha\in(1,2]$. We consider the critical Bernoulli bond percolation model on a Boltzmann map in the dilute and generic regimes $\alpha \in (3/2,2]$, and show that the open percolation cluster of the origin is itself a Boltzmann map in the dense regime $\alpha \in (1,3/2)$, with parameter \[\alpha':= \frac{2\alpha+3}{4\alpha-2}.\] This is the counterpart in random planar maps of the duality property $\kappa \leftrightarrow 16/\kappa$ of Schramm--Loewner Evolutions and Conformal Loop Ensembles, recently established by Miller, Sheffield and Werner \cite{miller_cle_2017}. As a byproduct, we identify the scaling limit of the boundary of the percolation cluster conditioned to have a large perimeter. The cases of subcritical and supercritical percolation are also discussed. In particular, we establish the sharpness of the phase transition through the tail distribution of the size of the percolation cluster.

with Cyril Marzouk PDF Published in ECP
The peeling process is an algorithmic procedure that discovers a random planar map step by step. In generic cases such as the UIPT or the UIPQ, it is known that any peeling process will eventually discover the whole map. In this paper we study the probability that the origin is not swallowed by the peeling process until time $n$ and show it decays at least as $n^{-2c/3}$ where
\[c \approx 0.12831235141783245423674486573872854933142662048339843...
\]
is defined via an integral equation derived using the Lamperti representation of the spectrally negative $3/2$-stable Lévy process conditioned to remain positive which appears as a scaling limit for the perimeter process. As an application we sharpen the upper bound of the sub-diffusivity exponent for random walk.
with Tom Hutchcroft and Asaf Nachmias PDF Published in
We study the random planar map obtained from a critical, finite variance, Galton-Watson plane tree by adding the horizontal connections between successive vertices at each level. This random graph is closely related to the well-known causal dynamical triangulation that was introduced by Ambjorn and Loll and has been studied extensively by physicists. We prove that the horizontal distances in the graph are smaller than the vertical distances, but only by a subpolynomial factor: The diameter of the set of vertices at level $n$ is both $o(n)$ and $n^{1+o(1)}$. This enables us to prove that the spectral dimension of the infinite version of the graph is almost surely equal to 2, and consequently that the random walk is diffusive almost surely. We also initiate an investigation of the case in which the offspring distribution is critical and belongs to the domain of attraction of an $\alpha$-stable law for $\alpha \in (1,2)$, for which our understanding is much less complete.


with Olivier Bernardi and Grégory Miermont PDF Published in Canadian J. Math
We study the percolation model on Boltzmann triangulations using a generating function approach. More precisely, we consider a Boltzmann model on the set of finite planar triangulations, together with a percolation configuration (either site-percolation or bond-percolation) on this triangulation.
By enumerating triangulations with boundaries according to both the boundary length and the number of vertices/edges on the boundary, we are able to identify a phase transition for the geometry of the origin cluster.
For instance, we show that the probability that a percolation interface has length $n$ decays exponentially with $n$ except at a particular value $p_c$ of the percolation parameter $p$ for which the decay is polynomial (of order $n^{-10/3}$). Moreover, the probability that the origin cluster has size $n$ decays exponentially if $p < p_c$ and polynomially if $p\geq p_c$.
The critical percolation value is $$ p_c=1/2 \mbox{ for site percolation, and} \ \ p_c=\frac{2\sqrt{3}-1}{11} \mbox{ for bond percolation.}$$ These values coincide with critical percolation thresholds for infinite triangulations identified by Angel for site-percolation, and by Angel & Curien for bond-percolation, and we give an independent derivation of these percolation thresholds.
Lastly, we revisit the criticality conditions for random Boltzmann maps, and argue that at $p_c$, the percolation clusters conditioned to have size $n$ should converge toward the stable map of parameter $ \frac{7}{6}$ introduced by Le Gall & Miermont. This enables us to derive heuristically some new critical exponents.
The critical percolation value is $$ p_c=1/2 \mbox{ for site percolation, and} \ \ p_c=\frac{2\sqrt{3}-1}{11} \mbox{ for bond percolation.}$$ These values coincide with critical percolation thresholds for infinite triangulations identified by Angel for site-percolation, and by Angel & Curien for bond-percolation, and we give an independent derivation of these percolation thresholds.
Lastly, we revisit the criticality conditions for random Boltzmann maps, and argue that at $p_c$, the percolation clusters conditioned to have size $n$ should converge toward the stable map of parameter $ \frac{7}{6}$ introduced by Le Gall & Miermont. This enables us to derive heuristically some new critical exponents.

with Timothy Budd and Cyril Marzouk PDF Published in J. Ecole Polytechnique
We study the geometry of infinite random Boltzmann planar maps having weight of polynomial decay of order $k^{-2}$ for each vertex of degree $k$. These correspond to the dual of the discrete "stable maps" of Le Gall and Miermont [Scaling limits of random planar maps with large faces, Ann. Probab. 39, 1 (2011), 1-69] studied in [Budd & Curien, Geometry of infinite planar maps with high degrees, Electron. J. Probab.] related to a symmetric Cauchy process, or alternatively to the maps obtained after taking the gasket of a critical $O(2)$-loop model on a random planar map. We show that these maps have a striking and uncommon geometry. In particular we prove that the volume of the ball of radius $r$ for the graph distance has an intermediate rate of growth and scales as $e^{\sqrt{r}}$. We also perform first passage percolation with exponential edge-weights and show that the volume growth for the fpp-distance scales as $e^r$. Finally we consider site percolation on these lattices: although percolation occurs only at $p=1$, we identify a phase transition at $p=1/2$ for the length of interfaces. On the way we also prove new estimates on random walks attracted to an asymmetric Cauchy process.

with Linxiao Chen and Pascal Maillard PDF Published in
We study the branching tree of the perimeters of the nested loops in critical $O(n)$ model for $n \in (0,2)$ on random quadrangulations. We prove that after renormalization it converges towards an explicit continuous multiplicative cascade whose offspring distribution $(x_i)_{i \geq 1}$ is related to the jumps of a spectrally positive $\alpha$-stable Lévy process with $\alpha= \frac{3}{2} \pm \frac{1}{\pi} \arccos(n/2)$ and for which we can compute explicitly the transform
$$ \mathbb{E}\left[ \sum_{i \geq 1}(x_i)^\theta \right] = \frac{\sin(\pi (2-\alpha))}{\sin (\pi (\theta - \alpha))} \quad \mbox{for }\theta \in (\alpha, \alpha+1).$$
An important ingredient in the proof is a new formula on first moments of additive functionals of the jumps of a left-continuous random walk stopped at a hitting time.

with Gady Kozma, Vladas Sidoravicius and Laurent Tournier PDF Published in Annales Inst. Henri Poincaré (D)
Consider the graph obtained by superposition of an independent pair of uniform infinite
non-crossing perfect matchings of the set of integers. We prove that this graph contains at most
one infinite path. Several motivations are discussed..

with Alessandra Caraceni PDF Published in the festschrift in honor of Chuck Newman's 70th birthday
We study an annealed model of Uniform Infinite Planar Quadrangulation (UIPQ) with an infinite two-sided self-avoiding walk (SAW), which can also be described as the result of glueing together two independent uniform infinite quadrangulations of the half-plane (UIHPQs). We prove a lower bound on the displacement of the SAW which, combined with estimates from our previous paper, shows that the self-avoiding walk is diffusive. As a byproduct this implies that the volume growth exponent of the lattice in question is 4 (as is the case for the standard UIPQ); nevertheless, using our previous work we show its law to be singular with respect to that of the standard UIPQ, that is -- in the language of statistical physics -- the fact that disorder holds.

with Jean Bertoin, Timothy Budd and Igor Kortchemski PDF
Published in PTRF
The purpose of the present work is twofold. First, we develop the theory of general self-similar growth-fragmentation processes by focusing on martingales which appear naturally in this setting. As an application, we establish many-to-one formulas for growth-fragmentations and define the notion of intrinsic area of a growth-fragmentation. Second, we identify a distinguished family of growth-fragmentations closely related to stable Levy processes, which are then shown to arise as the scaling limit of the perimeter process in Markovian explorations of certain random planar maps with large degrees (which are, roughly speaking, the dual maps of the stable maps of Le Gall & Miermont). This generalizes a geometric connection between large Boltzmann triangulations and a certain growth-fragmentation process, which was established in arXiv:1507.02265 .


with Timothy Budd PDF
Published in Electronic J. of Probab.
We study the geometry of infinite random Boltzmann planar maps with vertices of high degree. These correspond to the duals of the Boltzmann maps associated to a critical weight sequence $(q_k)_{k \geq 1}$ for the faces with polynomial decay $k^a$ with $a \in (3/2,5/2)$ which have been studied by Le Gall & Miermont as well as by Borot, Bouttier & Guitter. We show the existence of a phase transition for the geometry of these maps at a=2. In the dilute phase corresponding to $a \in (2,5/2)$ we prove that the volume of the ball of radius r (for the graph distance) is of order $r^d$ with $$d=\frac{a-1/2}{a-2},$$ and we provide distributional scaling limits for the volume and perimeter process. In the dense phase corresponding to $a \in (3/2,2)$ the volume of the ball of radius $r$ is exponential in $r$. We also study the first-passage percolation (FPP) distance with exponential edge weights and show in particular that in the dense phase the FPP distance between the origin and infinity is finite. The latter implies in addition that the random lattices in the dense phase are transient. The proofs rely on the recent peeling process introduced in arXiv:1506.01590 and use ideas of arXiv:1412.5509 in the dilute phase.

with Jean-François Le Gall PDF
Published in Annales Scientifiques de l'ENS
We study local modifications of the graph distance in large random triangulations. Our main results show that, in large scales, the modified distance behaves like a deterministic constant $c \in (0,\infty)$ times the usual graph distance. This applies in particular to the first-passage percolation distance obtained by assigning independent random weights to the edges of the graph. We also consider the graph distance on the dual map, and the first-passage percolation on the dual map with exponential edge weights, which is closely related to the so-called Eden model. In the latter two cases, we are able to compute explicitly the constant c by using earlier results about asymptotics for the peeling process. In general however, the constant c is obtained from a subadditivity argument in the infinite half-plane model that describes the asymptotic shape of the triangulation near the boundary of a large ball. Our results apply in particular to the infinite random triangulation known as the UIPT, and show that balls of the UIPT for the modified distance are asymptotically close to balls for the graph distance.
with Alessandra Caraceni PDF
Published in Random Structures and Algorithms
We give a new construction of the uniform infinite half-planar quadrangulation with a general boundary (or UIHPQ), analogous to the construction of the UIPQ presented by Chassaing and Durhuus, which allows us to perform a detailed study of its geometry. We show that the process of distances to the root vertex read along the boundary contour of the UIHPQ evolves as a particularly simple Markov chain and converges to a pair of independent Bessel processes of dimension 5 in the scaling limit. We study the "pencil" of infinite geodesics issued from the root vertex as Ménard, Miermont and the second author did for the UIPQ, and prove that it induces a decomposition of the UIHPQ into three independent submaps. We are also able to prove that balls of large radius around the root are on average $7/9$ times as large as those in the UIPQ, both in the UIHPQ and in the UIHPQ with a simple boundary; this fact we use in a companion paper to study self-avoiding walks on large quadrangulations.
with Jean Bertoin and Igor Kortchemski PDF
Published in Annals of Probab.
We are interested in the cycles obtained by slicing at all heights random Boltzmann triangulations with a simple boundary. We establish a functional invariance principle for the lengths of these cycles, appropriately rescaled, as the size of the boundary grows. The limiting process is described using a self-similar growth-fragmentation process with explicit parameters. To this end, we introduce a branching peeling exploration of Boltzmann triangulations, which allows us to identify a crucial martingale involving the perimeters of cycles at given heights. We also use a recent result concerning self-similar scaling limits of Markov chains on the nonnegative integers. A motivation for this work is to give a new construction of the Brownian map from a growth-fragmentation process.


with Jean-François Le Gall PDF
Published in Ann. Institut Henri Poincaré
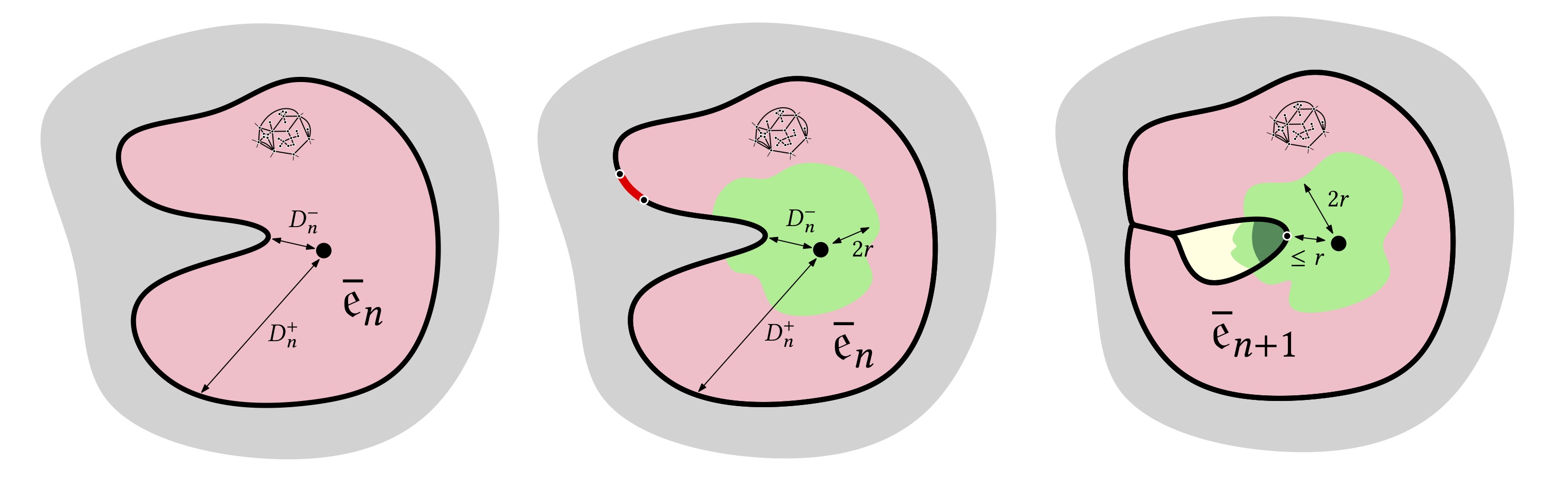
We study the scaling limit of the volume and perimeter of the discovered regions in the Markovian explorations known as peeling processes for infinite random planar maps such as the uniform infinite planar triangulation (UIPT) or quadrangulation (UIPQ). In particular, our results apply to the metric exploration or peeling by layers algorithm, where the discovered regions are (almost) completed balls, or hulls, centered at the root vertex. The scaling limits of the perimeter and volume of hulls can be expressed in terms of the hull process of the Brownian plane studied in our previous work. Other applications include the metric exploration of the dual graph of our infinite random lattices, and first-passage percolation with exponential edge weights on the dual graph, also known as the Eden model or uniform peeling.
with Bénédicte Haas PDF
Published in Annales de l'Institut Fourier
We study a general procedure that builds random real trees by gluing recursively a new branch on a uniform point of the pre-existing tree. The aim of this paper is to see how the asymptotic behavior of the sequence of lengths of branches influences some geometric properties of the limiting tree, such as compactness and Hausdorff dimension. In particular, when the sequence of lengths of branches behaves roughly like $n^{-a}$ for some $a \in (0,1]$, we show that the limiting tree is a compact random tree of Hausdorff dimension $ 1/a$. This encompasses the famous construction of the Brownian tree of Aldous. When $a>1$, the limiting tree is thinner and its Hausdorff dimension is always 1. In that case, we show that $1/a$ corresponds to the dimension of the set of leaves of the tree.
with Jean-François Le Gall PDF
Published in PTRF
We study the random metric space called the Brownian plane, which is closely related to the Brownian map and is conjectured to be the universal scaling limit of many discrete random lattices such as the uniform infinite planar triangulation. We obtain a number of explicit distributions for the Brownian plane. In particular, we consider, for every $r>0$, the hull of radius $r$, which is obtained by "filling in the holes" in the ball of radius $r$ centered at the root. We introduce a quantity $Z_r$ which is interpreted as the (generalized) length of the boundary of the hull of radius $r$. We identify the law of the process $(Z_r)_{r>0}$ as the time-reversal of a continuous-state branching process starting from infinity at time - infinity and conditioned to hit 0 at time 0, and we give an explicit description of the process of hull volumes given the process $(Z_r)$. We obtain an explicit formula for the Laplace transform of the volume of the hull of radius $r$, and we also determine the conditional distribution of this volume given the length of the boundary. Our proofs involve certain new formulas for super-Brownian motion and the Brownian snake in dimension one, which are of independent interest.
with Thomas Duquesne, Igor Kortchemski and Ioan Manolescu PDF
Published in J. Ecole Polytechnique
We are interested in the asymptotics of random trees built by linear preferential attachment, also known in the literature as Barabasi-Albert trees or plane-oriented recursive trees. We first prove a conjecture of Bubeck, Mossel & Racz concerning the influence of the seed graph on the asymptotic behavior of such trees. Separately we study the geometric structure of nodes of large degrees in a plane version of Barabasi-Albert trees via their associated looptrees. As the number of nodes grows, we show that these looptrees, appropriately rescaled, converge in the Gromov-Hausdorff sense towards a random compact metric space which we call the Brownian looptree. The latter is constructed as a quotient space of Aldous' Brownian Continuum Random Tree and is shown to have almost sure Hausdorff dimension 2.
PDF
Published in PTRF
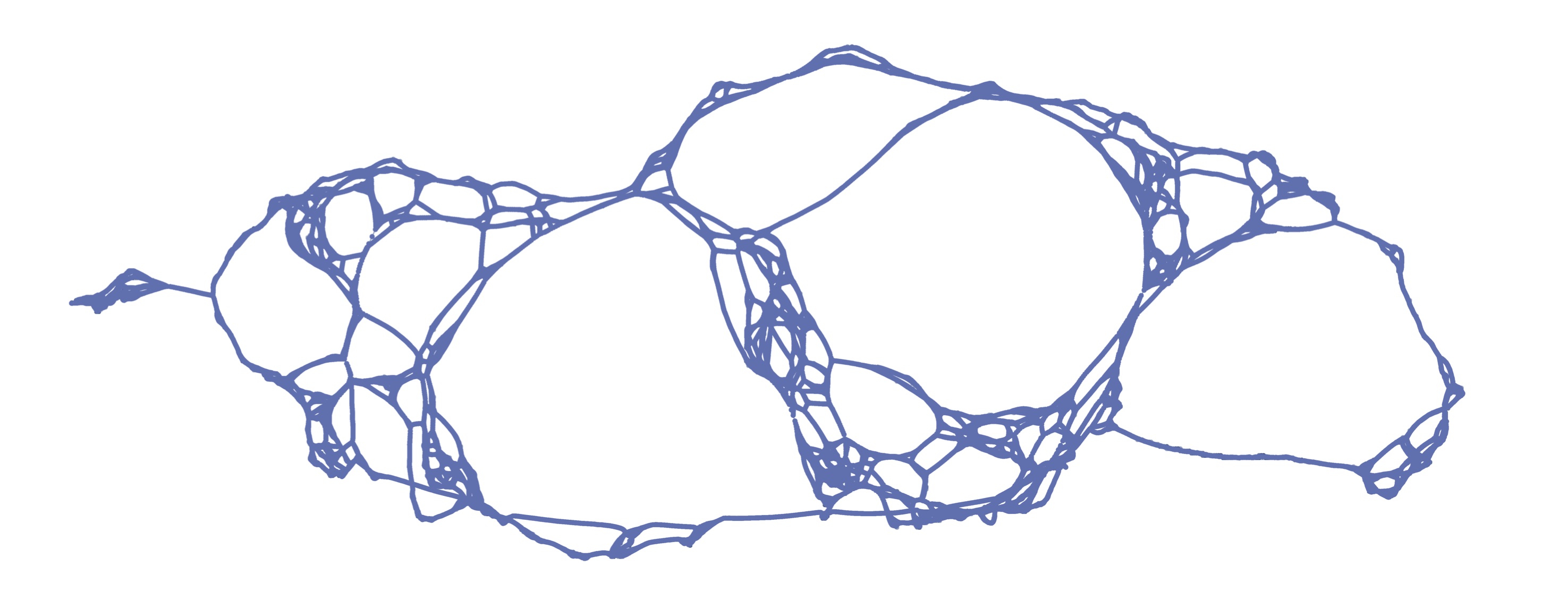
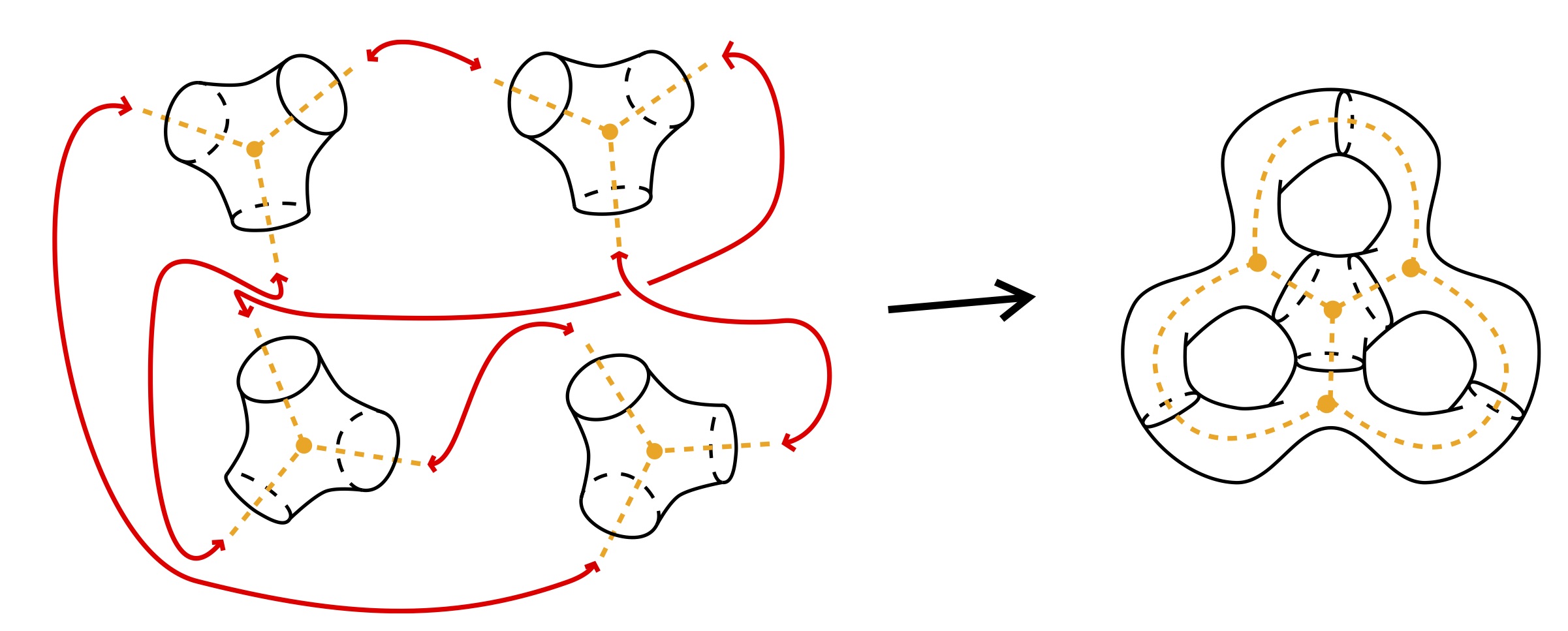
Pursuing the approach of Angel & Ray, we introduce and study a family of random infinite triangulations of the full-plane that satisfy a natural spatial Markov property. These new random lattices naturally generalize Angel & Schramm's Uniform Infinite Planar Triangulation (UIPT) and are hyperbolic in flavor. We prove that they exhibit a sharp exponential volume growth, are non-Liouville, and that the simple random walk on them has positive speed almost surely. We conjecture that these infinite triangulations are the local limits of uniform triangulations whose genus is proportional to the size.

with Omer Angel, Guillaume Chapuy and Gourab Ray PDF Published in ECP
We show that the local limit of unicellular maps whose genus is proportional to the number of edges is a supercritical geometric Galton-Watson tree conditioned to survive. The proof relies on enumeration results obtained via the recent bijection given by the second author together with Feray and Fusy.
PDF
We present a way to study the conformal structure of random planar maps. The main idea is to explore the map along an SLE (Schramm--Loewner evolution) process of parameter k=6 and to combine the locality property of the SLE_{6} together with the spatial Markov property of the underlying lattice in order to get a non-trivial geometric information. We follow this path in the case of the conformal structure of random triangulations with a boundary. Under a reasonable assumption called (*) that we have unfortunately not been able to verify, we prove that the limit of uniformized random planar triangulations has a fractal boundary measure of Hausdorff dimension 13 almost surely. This agrees with the physics KPZ predictions and represents a first step towards a rigorous understanding of the links between random planar maps and the Gaussian free field (GFF).
with Igor Kortchemski PDF Published in PTRF
We study site percolation on Angel & Schramm's uniform infinite planar triangulation. We compute several critical and near-critical exponents, and describe the scaling limit of the boundary of large percolation clusters in all regimes (subcritical, critical and supercritical). We prove in particular that the scaling limit of the boundary of large critical percolation clusters is the random stable looptree of index 3/2, which was introduced in a companion paper. We also give a conjecture linking looptrees of any index in (1,2) with scaling limits of cluster boundaries in random triangulations decorated with O(N) models.
with Bénédicte Haas and Igor Kortchemski PDF Published in Rand. Struc. Algo.
We study the graph structure of large random dissections of polygons sampled according to Boltzmann weights, which encompasses the case of uniform dissections or uniform p-angulations. As their number of vertices n goes to infinity, we show that these random graphs, rescaled by $n^{-1/2}$, converge in the Gromov--Hausdorff sense towards a multiple of Aldous' Brownian tree when the weights decrease sufficiently fast. The scaling constant depends on the Boltzmann weights in a rather amusing and intriguing way, and is computed by making use of a Markov chain which compares the length of geodesics in dissections with the length of geodesics in their dual trees.
with Jean-François Le Gall PDF Published in AOP
We study properties of the harmonic measure of balls in typical large discrete trees. For a ball of radius n centered at the root, we prove that, although the size of the boundary is of order $n$, most of the harmonic measure is supported on a boundary set of size approximately equal to $n^\beta$, where ${\beta} =0.78$... is a universal constant. To derive such results, we interpret harmonic measure as the exit distribution of the ball by simple random walk on the tree, and we first deal with the case of critical Galton-Watson trees conditioned to have height greater than n. An important ingredient of our approach is the analogous continuous model (related to Aldous' continuum random tree), where the dimension of harmonic measure of a level set of the tree is equal to $\beta$, whereas the dimension of any level set is equal to 1. The constant ${\beta}$ is expressed in terms of the asymptotic distribution of the conductance of large critical Galton-Watson trees
with Igor Kortchemski PDF Published in EJP
We introduce a class of random compact metric spaces $L(\alpha)$ indexed by $\alpha \in (1,2)$ and which we call stable looptrees. They are made of a collection of random loops glued together along a tree structure, and can be informally be viewed as dual graphs of $\alpha$-stable L\'evy trees. We study their properties and prove in particular that the Hausdorff dimension of $L(\alpha)$ is almost surely equal to $\alpha$. We also show that stable looptrees are universal scaling limits, for the Gromov-Hausdorff topology, of various combinatorial models. In a companion paper, we prove that the stable looptree of parameter 3/2 is the scaling limit of cluster boundaries in critical site-percolation on large random triangulations.
with Omer Angel PDF Published in Ann. Instit. Henri Poincaré
We study Bernoulli percolations on random lattices of the half-plane obtained as local limit of uniform planar triangulations or quadrangulations. Using the characteristic spatial Markov property or peeling process of these random lattices we prove a surprisingly simple universal formula for the critical threshold for bond and face percolations on these graphs. Our techniques also permit us to compute off-critical and critical exponents related to percolation clusters such as the volume and the perimeter.
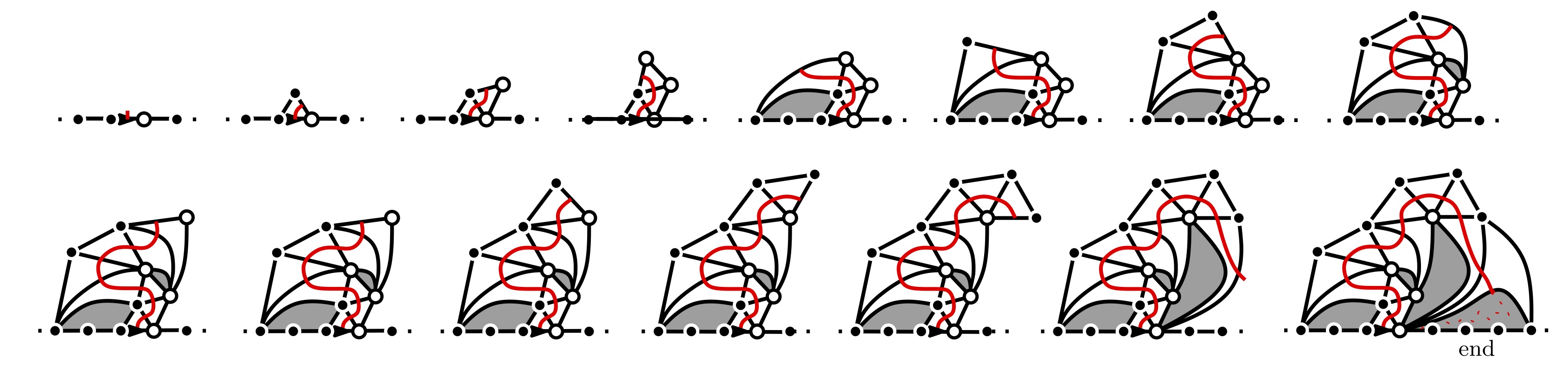

with Bénédicte Haas PDF Published in PTRF
We show that we can construct simultaneously all the stable trees as a nested family. More precisely, if $1 \le a \le a' \leq 2$ we prove that hidden inside any $a$-stable we can find a version of an $a'$-stable tree rescaled by an independent Mittag-Leffler type distribution. This tree can be explicitly constructed by a pruning procedure of the underlying stable tree or by a modification of the fragmentation associated with it. Our proofs are based on a recursive construction due to Marchal which is proved to converge almost surely towards a stable tree.
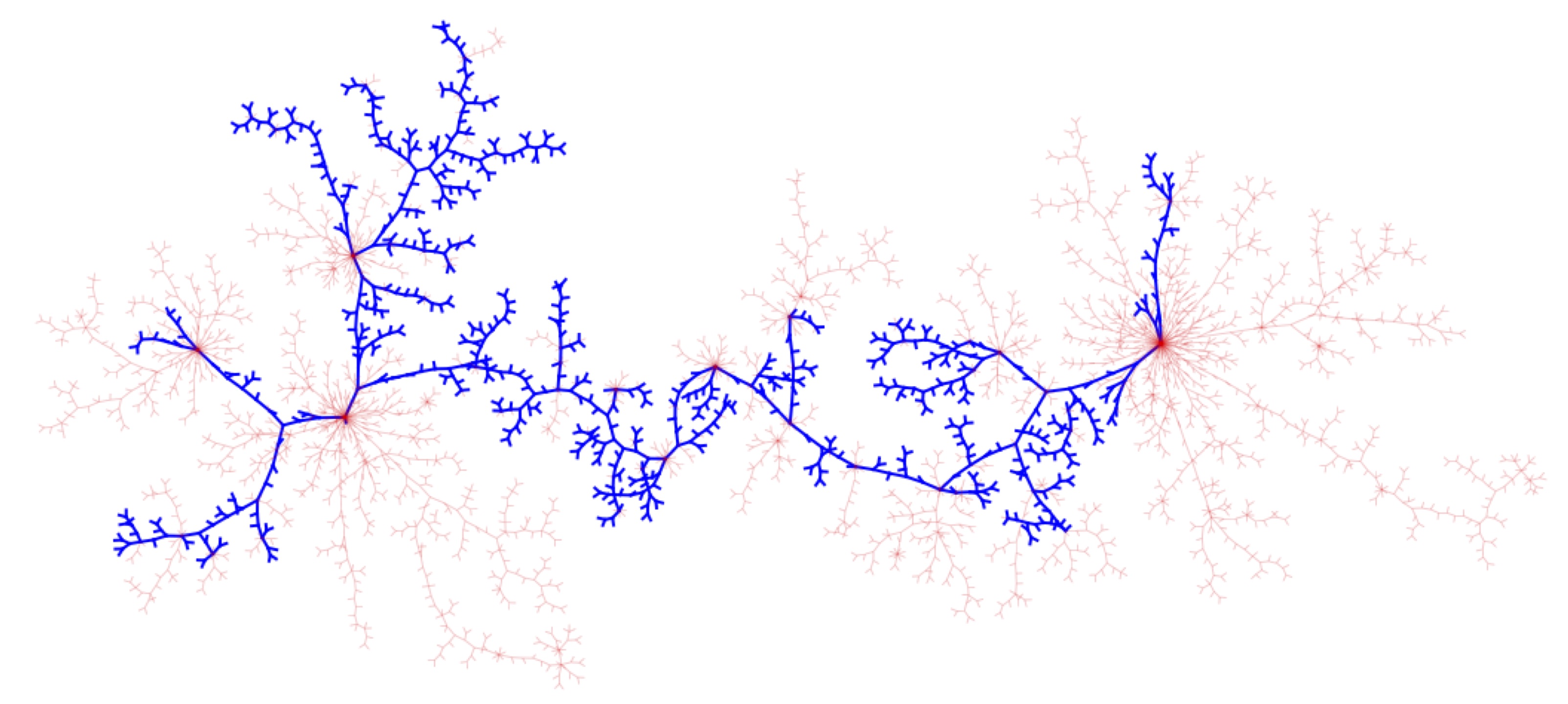

with Jean-François Le Gall PDF Published in J. Theoret. Prob.
We introduce and study the random non-compact metric space called the Brownian plane, which is obtained as the scaling limit of the uniform infinite planar quadrangulation. Alternatively, the Brownian plane is identified as the Gromov-Hausdorff tangent cone in distribution of the Brownian map at its root vertex, and it also arises as the scaling limit of uniformly distributed (finite) planar quadrangulations with n faces when the scaling factor tends to 0 less fast than $n^{-1/4}$. We discuss various properties of the Brownian plane. In particular, we prove that the Brownian plane is homeomorphic to the plane, and we get detailed information about geodesic rays to infinity.
with Itai Benjamini and Agelos Georgakopoulos PDF Published in ECP
It is shown that if a planar graph admits no non-constant bounded harmonic functions then the trajectories of two independent simple random walks intersect almost surely.

with Itai Benjamini PDF Published in GAFA
We study the pioneer points of the simple random walk on the uniform infinite planar quadrangulation (UIPQ) using an adaptation of the peeling procedure of Angel to the quadrangulation case. Our main result is that, up to polylogarithmic factors, $n^3$ pioneer points have been discovered before the walk exits the ball of radius n in the UIPQ. As a result we verify the KPZ relation in the particular case of the pioneer exponent and prove that the walk is subdiffusive with exponent less than 1/3. Along the way, new geometric controls on the UIPQ are established.
with Grégory Miermont PDF Published in Rand. Struc. Algo.
We introduce and study the uniform infinite planar quadrangulation (UIPQ) with a boundary via an extension of the construction of arXiv:1201.1052. We then relate this object to its simple boundary analog using a pruning procedure. This enables us to study the aperture of these maps, that is, the maximal distance between two points on the boundary, which in turn sheds new light on the geometry of the UIPQ. In particular we prove that the self-avoiding walk on the UIPQ is diffusive.
with Igor Kortchemski PDF Published in Rand. Struct. Algo.
We study various models of random non-crossing configurations consisting of diagonals of convex polygons, and focus in particular on uniform dissections and non-crossing trees. For both these models, we prove convergence in distribution towards Aldous' Brownian triangulation of the disk. In the case of dissections, we also refine the study of the maximal vertex degree and validate a conjecture of Bernasconi, Panagiotou and Steger. Our main tool is the use of an underlying Galton-Watson tree structure.
with Laurent Ménard and Grégory Miermont PDF
Published in Lat. Am. J. Probab. Math. Stat.
We introduce a new construction of the Uniform Infinite Planar Quadrangulation (UIPQ). Our approach is based on an extension of the Cori-Vauquelin-Schaeffer mapping in the context of infinite trees, in the spirit of previous work. However, we release the positivity constraint on the labels of trees which was imposed in these references, so that our construction is technically much simpler. This approach allows us to prove the conjectures of Krikun pertaining to the "geometry at infinity" of the UIPQ, and to derive new results about the UIPQ, among which a fine study of infinite geodesics.
with Takis Konstantopoulos PDF
Published in J. Theoret. Probab.
Let $B_1,B_2, $... be independent one-dimensional Brownian motions defined over the whole real line such that $B_i(0)=0$. We consider the nth iterated Brownian motion $$W_n(t)= B_n(B_{n-1}(...(B_2(B_1(t)))...)).$$ Although the sequences of processes $(W_n)$ do not converge in a functional sense, we prove that the finite-dimensional marginals converge. As a consequence, we deduce that the random occupation measures of $W_n$ converge towards a random probability measure $\mu_\infty$. We then prove that $\mu_\infty$ almost surely has a continuous density which must be thought of as the local time process of the infinite iteration of independent Brownian motions.

PDF Published in Comb. Probab. Comp.
We prove that the rescaled costs of partial match queries in a random two-dimensional quadtree converge almost surely towards a random limit which is identified as the terminal value of a martingale. Our approach shares many similarities with the theory of self-similar fragmentations.


with Itai Benjamini PDF Published in ECP
We use the concept of unimodular random graph to show that the branching simple random walk on $\mathbb{Z}^d$, indexed by a critical geometric Galton-Watson tree conditioned to survive is recurrent if and only if $d\leq4$.
with Wendelin Werner PDF Published in J. EMS
We construct and study the unique random tiling of the hyperbolic plane into ideal hyperbolic triangles (with the three corners located on the boundary) that is invariant (in law) with respect to Moebius transformations, and possesses a natural spatial Markov property that can be roughly described as the conditional independence of the two parts of the triangulation on the two sides of the edge of one of its triangles.


with Yuval Peres PDF Published in ECP
We consider multitype branching processes arising in the study of random laminations of the disk. We classify these processes according to their subcritical or supercritical behavior and provide Kolmogorov-type estimates in the critical case corresponding to the random recursive lamination process of Curien & Le Gall. The proofs use the infinite dimensional Perron-Frobenius theory and quasi-stationary distributions.
with Jean-François Le Gall and Grégory Miermont PDF Published in Ann. Instit. Henri Poincaré
The cactus of a pointed graph is a discrete tree associated with this graph. Similarly, with every pointed geodesic metric space E, one can associate an $\mathbb{R}$-tree called the continuous cactus of E. We prove under general assumptions that the cactus of random planar maps distributed according to Boltzmann weights and conditioned to have a fixed large number of vertices converges in distribution to a limiting space called the Brownian cactus, in the Gromov-Hausdorff sense. Moreover, the Brownian cactus can be interpreted as the continuous cactus of the so-called Brownian map.
with Itai Benjamini PDF Published in EJP
A stationary random graph is a random rooted graph whose distribution is invariant under re-rooting along the simple random walk. We adapt the entropy technique developed for Cayley graphs and show in particular that stationary random graphs of subexponential growth are almost surely Liouville, that is, admit no non constant bounded harmonic function. Applications include the uniform infinite planar quadrangulation and long-range percolation clusters.
with Adrien Joseph PDF Published in J. Applied Probab.
We analyze the mean cost of the partial match queries in random two-dimensional quadtrees. The method is based on fragmentation theory. The convergence is guaranteed by a coupling argument of Markov chains, whereas the value of the limit is computed as the fixed point of an integral equation.

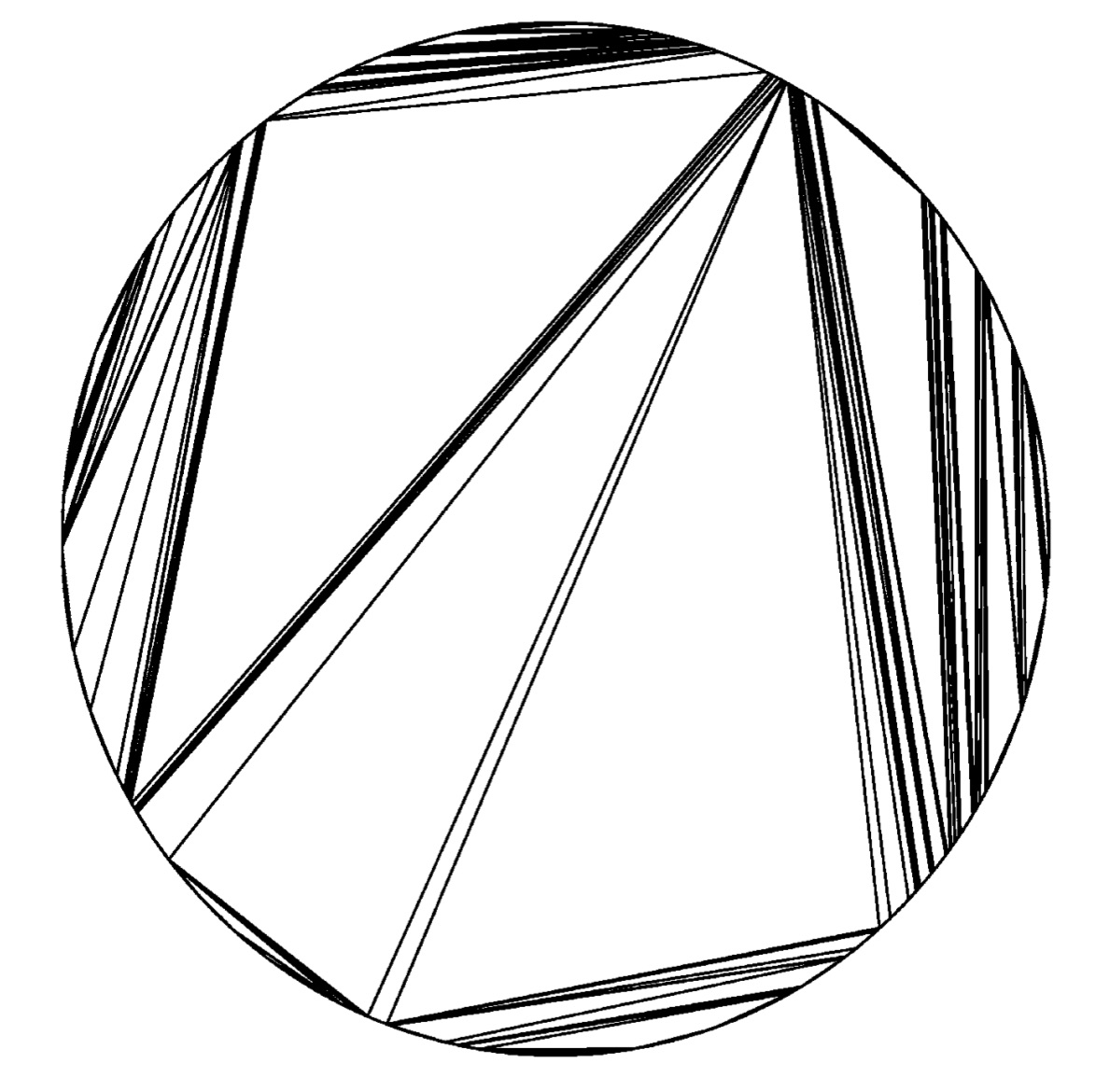
with Jean-François Le Gall PDF Published in AOP
We introduce and study an infinite random triangulation of the unit disk that arises as the limit of several recursive models. This triangulation is generated by throwing chords uniformly at random in the unit disk and keeping only those chords that do not intersect the previous ones. After throwing infinitely many chords and taking the closure of the resulting set, one gets a random compact subset of the unit disk whose complement is a countable union of triangles. We show that this limiting random set has Hausdorff dimension $b+1$, where $$b=(\sqrt{17}-3)/2,$$ and that it can be described as the geodesic lamination coded by a random continuous function which is Hölder continuous with exponent $b-\varepsilon$, for every $\varepsilon>0$. We also discuss recursive constructions of triangulations of the n-gon that give rise to the same continuous limit when n tends to infinity.

with Itai Benjamini PDF J. Europ. Combin.
The core of this note is the observation that links between circle packings of graphs and potential theory developed in Benjamini - Schramm and He - Schramm can be extended to higher dimensions. In particular, it is shown that every limit of finite graphs sphere packed in $\mathbb{R}^d$ with a uniformly-chosen root is d-parabolic. We then derive few geometric corollaries. E.g.\,every infinite graph packed in $\mathbb{R}^{d}$ has either strictly positive isoperimetric Cheeger constant or admits arbitrarily large finite sets W with boundary size which satisfies a d-dimensional isoperimetric inequality. Some open problems and conjectures are gathered at the end.
Le manuscrit de ma thèse réalisée sous la direction de Jean-Francois Le Gall est disponible ici.
Le manuscrit de mon HDR est disponible ici.
Le manuscrit de mon HDR est disponible ici.